
Определить все параметры треугольника без дополнительных построений практически никогда не удается. Эти конструкции представляют собой уникальные графические свойства треугольника, помогающие определить размеры сторон и углов.
Определение
Одним из таких свойств является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к противоположной его стороне. Вершина — это одна из трёх точек, которые вместе с тремя отрезками образуют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике невозможно провести высоту внутри треугольника. Как видно на рисунке 1, высота в данном случае внешняя. Кроме того, построение высоты в прямоугольном треугольнике – нестандартная ситуация. В этом случае две из трёх высот треугольника пройдут через катеты, а третья — от вершины к гипотенузе.
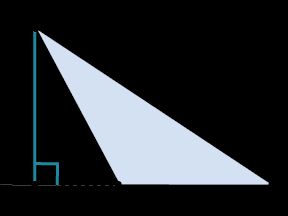
Обычно высоту треугольника обозначают буквой ч. Высота обозначается и другими цифрами.
Как найти высоту треугольника?
Существует три стандартных способа найти высоту треугольника:
Через теорему Пифагора
Этот метод применяется для равносторонних и равнобедренных треугольников. Давайте проанализируем решение для равнобедренного треугольника, а затем скажем, почему то же решение справедливо и для равностороннего треугольника.
Дано: равнобедренный треугольник ABC с основанием AC. АВ=5, АС=8. Найдите высоту треугольника.
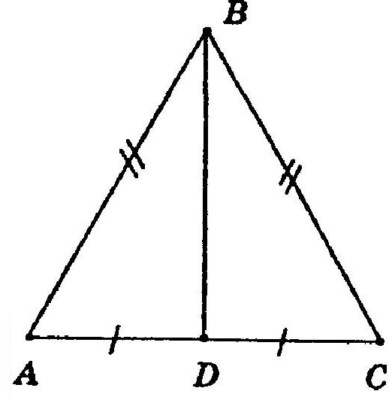
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенного к основанию:
- Высота совпадает с медианой и биссектрисой
- Делит основу на две равные части.
Обозначим высоту как ВD. Находим DC как половину основания, так как высота точки D делит основание пополам постоянный ток=4
Высота — перпендикуляр, а значит, BDC — прямоугольный треугольник, а высота BD — катет этого треугольника.
Найдем высоту по теореме Пифагора: $$BD=\sqrt{BC^2-HC^2}=\sqrt{25-16}=3$
Любой равносторонний треугольник является равнобедренным, только основание равно сторонам. То есть вы можете использовать ту же процедуру.
Через площадь треугольника
Этот метод можно использовать для любого треугольника. Чтобы им воспользоваться, нужно знать площадь треугольника и сторону, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны можно будет вычислить соответствующую высоту.
Формула площади треугольника: $$S={1\over2}*bh$$, где b — сторона треугольника, а h — высота, проведенная к этой стороне. Выразим высоту по формуле:
$$h=2*{S\over b}$
Если площадь 15, сторона 5, то высота $$h=2*{15\over5}=6$
Через тригонометрическую функцию
Третий способ подойдет, если известны сторона и угол при основании. Для этого нужно использовать тригонометрическую функцию.
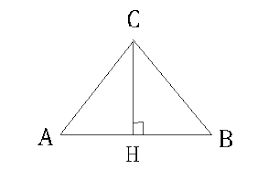
Угол ВСН=30 градусов, а сторона ВС=8. У нас все тот же прямоугольный BCH. Применим определение косинуса угла к прямоугольному треугольнику. Косинус острого угла – это отношение прилежащего катета к гипотенузе, что означает: BH/BC = cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна до 90 градусов.
Угол известен, как и сторона. Выразим высоту треугольника:
$$BH=BC*\cos (60\unicode{xb0})=8*{1\over2}=4$
Значение косинуса обычно берут из таблиц Брадиса, а вот значения тригонометрических функций для 30,45 и 60 градусов являются номерами таблиц.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Мы выделили типичные проблемы и записали три формулы высоты треугольника.








Комментирование закрыто