
Внешний угол треугольника редко используется при решении геометрических задач. Однако лучше знать свойства внешнего угла, поскольку рано или поздно перед каждым учеником встанет задача использования этих свойств.
Внешний угол
Внешний угол треугольника – это угол, примыкающий к внутреннему углу. В треугольнике три внутренних угла, их сумма равна 180 градусов. Смежные углы — это углы, у которых одна из сторон каждого лежит на одной прямой, а другая — общая.
Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого необходимо выполнить некоторую дополнительную конструкцию. Чтобы увидеть внешний угол треугольника, нужно вытянуть сторону. Каждая вершина имеет две стороны, соответственно две прямые могут быть продолжены, и будет два смежных угла.
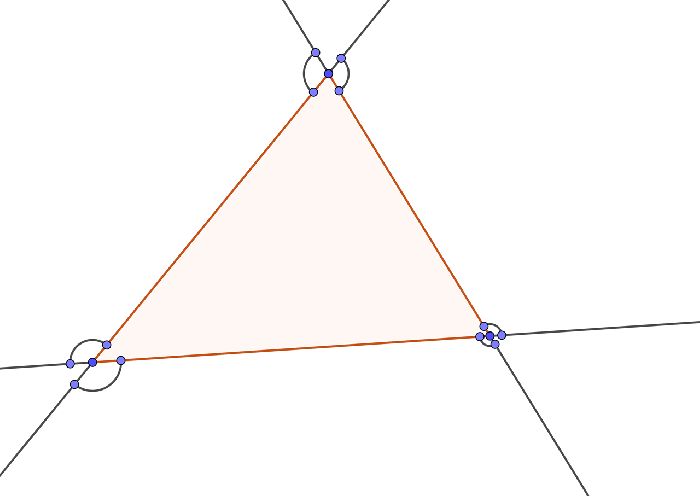
Всего у треугольника 6 внешних углов.
Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.
Свойства внешних углов
Свойства внешних углов треугольника не так уж и велики, и все они связаны с определением внешнего угла.
Фундаментальное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все та же 180. Итак, если обозначить внутренние углы a, b, c и внешний угол d, то:
а+б+с=180
а+д=180
Вычтем второе из первого выражения и получим:
а+b+c-(a+d)=180-180
б+кд=0
d=в+с – вот и все доказательства.
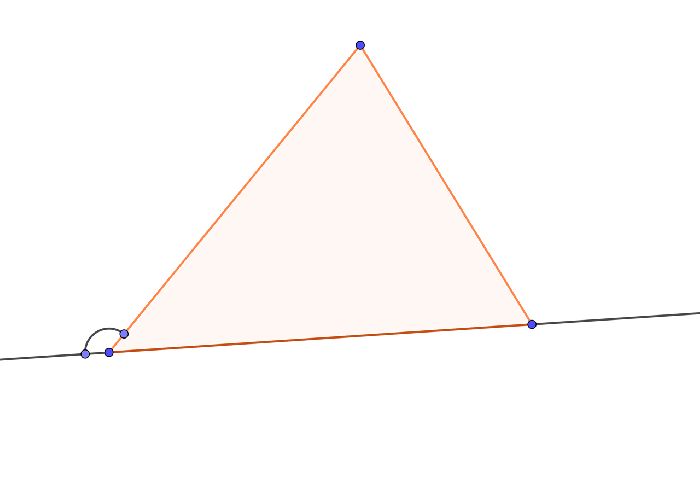
Есть несколько дополнительных свойств внешних углов:
- Если решение задачи требует одновременного существования двух внешних углов при одной вершине чертежа, можно заметить, что эти внешние углы будут равны, как и вертикальные.
- Сумма трех внешних углов, по одному при каждой вершине, равна 360 градусов.
- Поскольку внешний и внутренний углы треугольника смежные, их сумма равна 180 градусов.
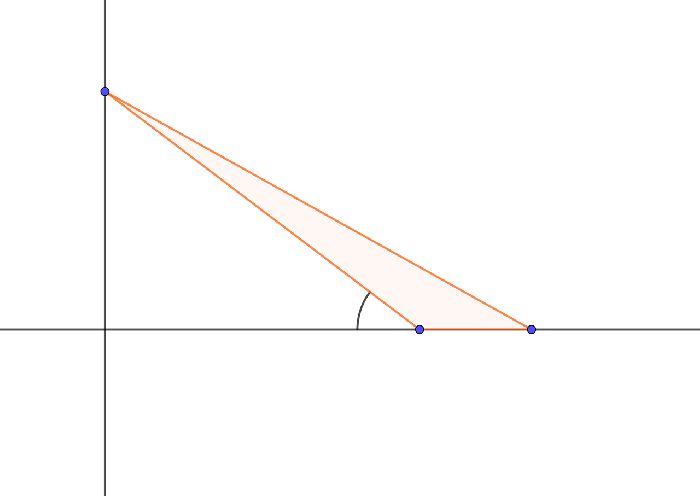
Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.
Что мы узнали?
Мы дали определение внешнего угла треугольника. В процессе решения задачи мы подсчитали количество внешних углов в треугольнике и определили функции путем построения внешних углов. Мы рассказали вам, где чаще всего используются свойства внешних углов треугольника.








Комментирование закрыто