
Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник необычным для восприятия. Это часто приводит к путанице, поэтому стоит рассмотреть разные варианты решения задач с нахождением параметров тупоугольного треугольника.
Определения
Тупоугольный треугольник – это любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но не может быть равносторонним или прямоугольным. Действительно, на этом характеристики этой фигуры заканчиваются. В остальном это обычный треугольник, и подход к решению таких фигур ничем не отличается.
В треугольнике сумма углов равна 180 градусов, поэтому только один угол в треугольнике может быть тупым, а два других всегда острые. Площадь тупоугольного треугольника находится так же, как и площадь любого треугольника.

Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Давайте рассмотрим несколько интересных задач поиска данных в тупоугольном треугольнике.
Пример решения задачи
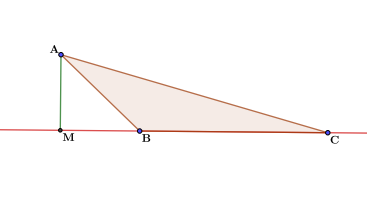
Есть несколько способов решить любую проблему. В этой ситуации можно перебрать площади треугольников, превратить тупоугольный треугольник в прямоугольный или воспользоваться теоремой косинусов. Каждый метод дает представление о том, как решать задачи о тупоугольном треугольнике. Давайте воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площади треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А может быть — как половина произведения двух сторон и синуса угла между ними. Мы знаем косинус угла, и по косинусу всегда можно найти синус.
$$sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-4 \over13}=\sqrt{9 \over13}={3\over\sqrt{13}}$
Теперь запишем две формулы площади, выразим через них высоту и найдем значение.
$$S={1\over2}*AM*BC$
$$S={1\over2}*AB*BC sin(ABC)$
$${1\over2}*AM*BC={1\over2}*AB*BC*sin(ABC)$
$$AM*BC=AB*BC*sin(ABC)$
$$AM=AB*sin(ABC)$
$$AM=\sqrt{13}*{3 \over \sqrt{13}}=3$
- Другой способ — превратить тупоугольный треугольник в прямоугольный. Если присмотреться, то вы заметите на рисунке два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ косинус угла АВМ можно найти по формулам приведения. Затем по значению косинуса найдите значение синуса для того же угла. А синус – это отношение противоположной стороны к гипотенузе. Противоположный катет – это искомая нами высота, а гипотенуза – сторона АВ прямоугольного треугольника.
$$cos(ABM)=cos(180-ABC)=-cos(ABC)$
$$cos(ABM)=-cos(ABC)={2\over \sqrt{13}}$
Тогда мы сможем выразить синус, как и в первом способе, через основное тригонометрическое тождество.
$$Sin(ABM)=\sqrt{1-cos(ABM)^2}=\sqrt{13-4\over13}=\sqrt{9\over13}={3\over\sqrt{13}}$
$$Sin(ABM)=AM/AB$
$$AM=AB*sin(ABM)=\sqrt{13}*{3\over\sqrt{13}}=3$
- Третий метод — теорема о синусе и косинусе. Чтобы использовать этот метод, мы найдем значение AC через теорему косинуса, затем через теорему синуса найдем синус угла ACB и определим AM от синуса угла ACB к большому прямому углу AMC.
$$AC=\sqrt{AB^2+BC^2-2AB*BC*cos(ABC)}=$
$$\sqrt {\sqrt{13}^2+2^2-2*\sqrt{13}*{-2\over\sqrt{13}}}=$
$$\sqrt{13+4+8}=\sqrt{25}=5$$ – по теореме косинусов.
$${AC\over{sin(ABC)}}={AB\over{sin(ACB)}}$$ – по теореме синуса.
Значение синуса угла ABC определим, используя основное тригонометрическое тождество.
$$ Sin(ABC)=\sqrt{1-cos^2(ABC)}=\sqrt{13-{4\over{4}}}=\sqrt{9\over{13}}={3\over \sqrt{13}}$
Выразим искомый синус угла АСВ.
$$Sin(ACB)=AB*{sin(ABC)\over{AC}}$
$$Sin(ACB)=(\sqrt{13}*{{3\over\sqrt{13}}\over{5}})={3\over5}$
Выразим сторону АМ из треугольника АМС и найденного значения синуса.
$$Sin(ACB)={AM\over AC}$
$$AM=грех(ACB)*AC$
$$AM={3\over5}*{5}=3$
Ответы всех трех методов совпали, а это значит, что задача решена правильно.
Что мы узнали?
Мы говорили об определении тупоугольного треугольника. Мы узнали и увидели на практике, какие существуют методы решения тупоугольных треугольников, а также выяснили, какие формулы и теоремы нужно знать, чтобы успешно решить тупоугольный треугольник.








Комментирование закрыто