
Равенство – это следующее понятие после равенства: как в математике после сложения следует умножение, так и в геометрии мы изучаем равенство после равенства треугольников. В реальной жизни сходство посредством теневых расчетов помогает определить реальные размеры зданий или высотных сооружений. В задачах на эту тему благодаря подобию можно найти значение сторон по известному соотношению.
Определения
Треугольники, у которых соотношения сторон одинаковы, называются равными. Предположим, треугольник ABC равен треугольнику DPH. Это означает, что:
$${AB\over{DP}}={BC\over{PH}}={AC\over{DH}}=k$
k это коэффициент подобия.
Для правильного треугольника существует три критерия подобия. Именно с их помощью доказываются признаки подобия прямоугольных треугольников.
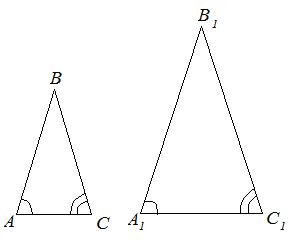
Первый признак равенства: в двух углах. Если два угла треугольника равны двум углам другого треугольника, то такие треугольники равны.
Остальные персонажи: с трех сторон. Если три стороны треугольника пропорциональны соответствующим сторонам другого треугольника, то такие треугольники подобны.
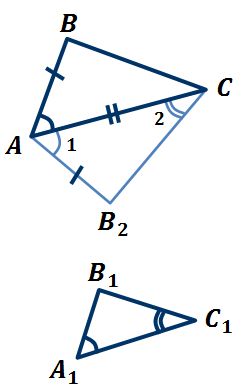
Третий знак: с обеих сторон и угол. Если две стороны треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны, то такие треугольники подобны.
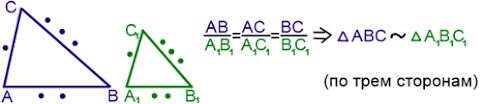
Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
- Первый признак острого угла: если острый угол прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
доказать этот признак очень легко. Достаточно помнить, что прямоугольный треугольник – это треугольник, содержащий прямой угол. Это означает, что у двух прямоугольных треугольников один из углов всегда равен другому. Причем один из острых углов также равен соответствующему углу в другом треугольнике. Это означает, что такие треугольники имеют два равных угла, причем треугольники равны по первому знаку равенства.
- Остальные персонажи: с двух сторон. Если два катета прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. Между двумя ногами всегда существует прямой угол. Это значит, что у нас есть две пропорциональные стороны и равные углы между ними. Тогда треугольники подобны по третьему критерию подобия.
- Третий признак: по катету и гипотенузе. Если катет и гипотенуза прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то треугольники подобны. Чтобы доказать знак, нужно вспомнить понятие косинуса. Косинус угла – это отношение прилежащего катета к гипотенузе.
$$cos(ACB)={BC\over{AC}}$
$$cos(DHP)={PH\over{DH}}$
Причём по условию: $${AC\over{DH}}={BC\over{PH}}$$. Из условия выражаем BC и заменяем его значением косинуса.
$$ВС=РН*{AC\over{DN}}$
$$cos(ACB)={BC\over{AC}}={PH*{AC\over{DH}}\over AC}={PH\over{AC}}$$ – то есть косинусы оба угла равны. Углы острые, значит, углы равны. Тогда треугольники равны по обеим сторонам и углу между ними.
Что мы узнали?
Мы проанализировали понятие сравнения, выделили все определения и теоремы, необходимые для доказательства трех признаков соответствия прямоугольных треугольников. Мы показали, что эти символы являются лишь следствием наиболее важных, т.е эти свойства призваны облегчить и ускорить решение. Это означает, что если вы вдруг забудете знаки прямоугольного треугольника, вы всегда сможете воспользоваться общими.








Комментирование закрыто