
Прямоугольные треугольники, наряду с равнобедренными и равносторонними треугольниками, занимают свое место среди треугольников, обладая особым набором специфических свойств, характерных только для этого типа треугольников. Мы рассмотрим несколько теорем о равенстве прямоугольных треугольников, которые существенно упрощают решение некоторых задач.
Первый признак равенства прямоугольных треугольников
Знаки равенства прямоугольных треугольников происходят от трёх знаков равенства треугольников, но прямой угол их искажает, скорее расширяет, упрощая. Любой из знаков равенства прямоугольных треугольников можно заменить одним из трех основных, но это займет слишком много времени, поэтому выбрано 5 свойств и знаков равенства прямоугольных треугольников.
Очень часто вместо использования основных признаков равенства треугольников, используется метод наложения, когда две фигуры мысленно накладываются одна на другую. Нельзя сказать, что это верно или неверно. Просто еще один способ доказательства, который стоит учитывать. Но нельзя думать, что любой признак можно доказать обычным наложением. Именно поэтому рассмотрим доказательство признаков равенства прямоугольных треугольников через три основных признака равенства треугольников.
Первый признак равенства прямоугольных треугольников: два прямоугольных треугольника равны, если два катета одного треугольника равны двум катетам другого треугольника. Коротко этот зызный поиск регенства по соседству с катетами.
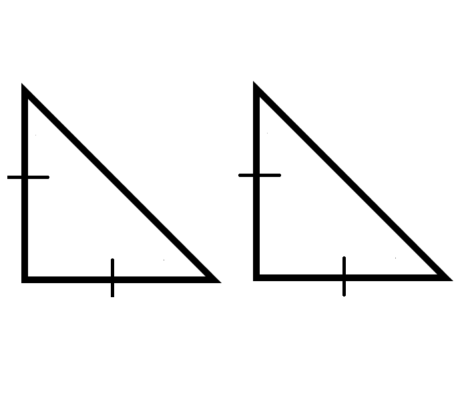
доказать эту особенность очень просто. Дано: два катета прямоугольного треугольника равны. Между катеми имеется прямой угол, равный 90 градусам, поэтому размеры углов в треугольниках совпадают. Следовательно, два треугольника равны двум сторонам и углу между ними.
Второй признак
Второй знак читается так: два прямоугольных треугольника равны, если сторона и прилежащий к ней острый угол одного треугольника равны стороне и прилежащему к ней острому углу другого треугольника.
Второй признак доказывается на основе того же утверждения о равенстве прямых углов между собой. Если стороны треугольника равны, острые углы равны и прямые углы равны по определению, то такие треугольники равны по второму знаку равенства (стороны и два прилежащих угла).
Третий признак
Два прямоугольных треугольника равны, если сторона и противолежащий ей острый угол одного треугольника равны стороне и противолежащему ему углу другого треугольника.
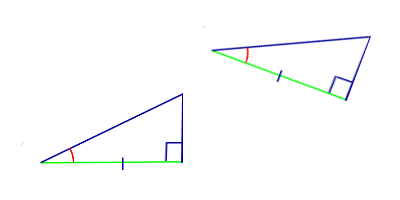
Сумма острых углов треугольника равна 90 градусам. Углы пометим маленькими латинскими буквами для простоты доказательства. Один угол прямой, а два других отмечены буквами a и b в первом треугольнике; c и d во втором треугольнике.
$$a+b=c+d$
Углы a и d в условиях задачи равны между собой.
$$а=d$
$$a+b=c+a$
Вычтем из разговора строн выражение угол a
$$b=c$
То есть, если в двух прямоугольных треугольниках два острых угла равны между собой, то два других острых угла также будут равны, и мы можем использовать второй знак.
Во втором и третьем признаке нужно особенно акцентировать внимание на остром угле, так как прямые углы всегда равны между собой.
Четвертый признак
Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Как было сказано в предыдущей примете: если острый угол прямоугольного треугольника равен соответствующему острому углу другого прямоугольного треугольника, то и другая пара острых углов треугольников будет равна.
Следовательно, при условии этого знака мы имеем равенство гипотенузы и двух острых углов треугольников, а, следовательно, такие треугольники будут равны вдоль стороны и двух прилежащих углов (2 знака равенства треугольников)
Пятый признак
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
Если гипотенуза и катеты двух треугольников соответственно равны, то и вторые катеты таких треугольников будут равны между собой. Это следует из теоремы Пифагора.
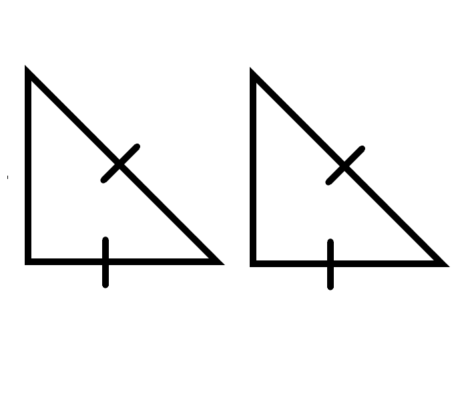
Квадрат гипотенузы ревен сумме квадратов катетов. Гипотенузы равны друг другу, катет одного треугольника равен катету другого треугольника, то есть сумма остается верной, а два других катета равны друг другу. А это соответствует третьему знаку равенства треугольников (по трем сторанам).
Что мы узнали?
Доказательство пяти знаков равенства треугольников мы рассмотрели через основные знаки равенства треугольников. Они обсудили, почему такое доказательство предпочтительнее навязывания, и определили путь доказательства, который позволит в любой момент восстановить в памяти основные понятия темы, без чрезмерного запоминания.








Комментирование закрыто