Прямоугольный знак

В этой статье мы поговорим о свойствах прямоугольника. Выделим наиболее важные из них и рассмотрим каждый отдельно.

Определения

Основная часть доказательства основана на том, что в четырехугольнике сумма углов равна 360 градусов.

Всего в прямоугольнике 7 символов. Чтобы их использовать, необходимо сначала запомнить определения:

Прямоугольник – это параллелограмм, у которого все углы прямые.

Параллелограмм – это выпуклый четырехугольник, у которого все стороны попарно равны и параллельны.

Для того, чтобы определить выпуклый четырехугольник или нет нужно последовательно проводить через каждую из сторон фигуры линию. Если в каждом из 4 случаев (поскольку сторон 4) вся фигура будет оставаться по одну сторону от линии, то четырехугольник выпуклый.

Признаки

Перед нами параллелограмм. Как доказать, что это прямоугольник? Используйте одного из персонажей:

  • Параллелограмм является прямоугольником, если один из углов прямой.

В параллелограмме противоположные углы равны. Это значит, что если один из углов прямой, то угол, противоположный ему, тоже прямой, а остальные два равны между собой. Сумма всех углов квадрата равна 360 градусов.

Два угла прямые, значит, остаётся 360-90*2=180. Эта сумма двух равных углов означает, что каждый из оставшихся углов прямой: 180/2=90. Если все углы в параллелограмме прямые, то это прямоугольник.

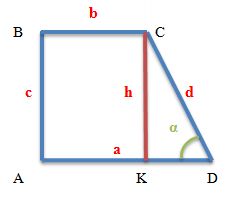
Этот признак работает только для параллелограммов. В случае с четырехугольниками прямой угол может быть и у прямоугольной трапеции.

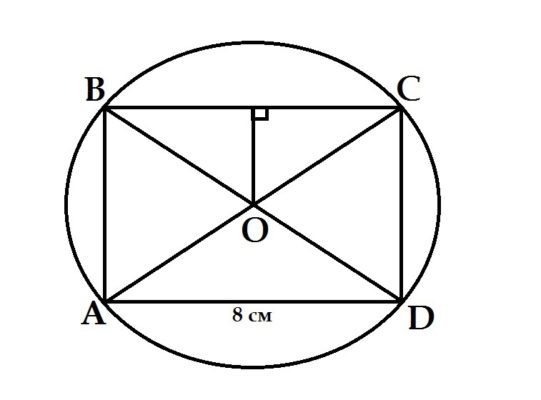
Прямоугольный знак

Рис. 1. Прямоугольная трапеция.
  • Если вокруг параллелограмма можно нарисовать круг, то это прямоугольник.

Чтобы описать круг вокруг квадрата, необходимо, чтобы сумма противоположных углов составляла 180 градусов. Противоположные углы в параллелограмме равны, поэтому каждый угол равен 180/2 = 90 градусов. Итак, это прямоугольник.

Прямоугольный знак

Рис. 2. Прямоугольник, вписанный в окружность.
  • Если все углы в квадрате равны, то это прямоугольник. Для этого знака не обязательно следить за тем, чтобы перед вами был параллелограмм. В любом квадрате сумма углов равна 360. Если все углы равны, то 360/4 = 90 градусов каждый из углов. Получается, что это все равно прямоугольник.
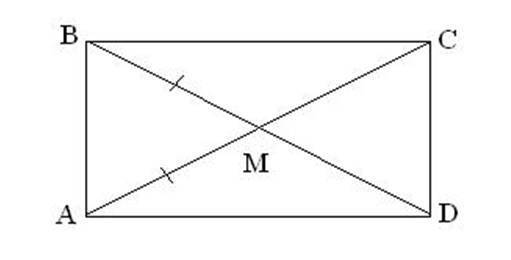
  • Если диагонали параллелограмма равны, то это прямоугольник. Чтобы доказать это, нарисуйте две диагонали и изучите полученные треугольники. Треугольники ABD и ACD равны по трем сторонам. У них общее основание, диагонали равны, а третья сторона — это две противоположные стороны параллелограмма, которые также равны между собой. Треугольники конгруэнтны, что означает, что их части конгруэнтны: смежные углы в параллелограмме равны, а это означает, что все углы в параллелограмме равны. Перед нами прямоугольник.

Прямоугольный знак

Рис. 3. Рисунок для доказательства.
  • Если квадрат имеет три прямых угла, то это прямоугольник. Если посчитать, то четвертый угол в этом случае будет равен: 360-90*3=90, то есть четвертый угол будет прямым.
  • Если квадрат диагонали равен сумме квадратов двух соседних сторон. В данном случае диагональ — это гипотенуза, а стороны — катеты прямоугольного треугольника согласно обратной теореме Пифагора (это один из признаков прямоугольного треугольника).

Это важные особенности прямоугольников. Есть и другие, относящиеся к уже перечисленным. И самое главное, помните, что в математике важны определения. Нарисуйте прямоугольный прямоугольник – неверная формулировка. Прямоугольник всегда был, есть и всегда будет прямоугольным.

Что мы узнали?

Мы узнали, как доказать, что параллелограмм или четырехугольник является параллелограммом, вспомнили некоторые определения и познакомились с ведущим методом определения прямоугольника – по углам.