
Плоскостность — основная единица планиметрии. Для проспприятия сложных фигур, таких как пирамида, конус или призма, необходимо понимать и, что немаловажно, представлять, что они плоские.
Определение плоскости
Плоскость представляет собой поверхность, содержащую прямые линии, соединяющие две ее точки. Это определение звучит довольно запутанно, поэтому лучше его запомните. А для понимания стоит вспомнить, что плоскость – это прямая поверхность. Любая грань пирамиды плоская, как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Фигуры в планиметрии составляются из плоскостей, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, состоящая из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Способы задания плоскостей
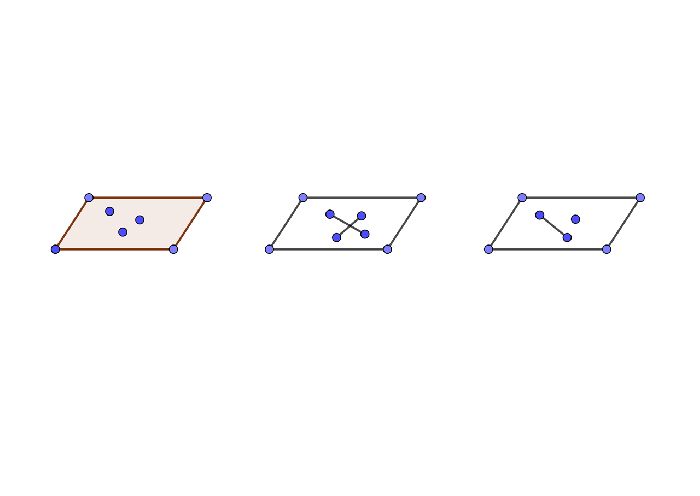
Плоскость можно определить тремя точками, не лежащими на одной прямой. Из этого утверждения остается еще два варианта указания плоскостей. В этом случае специального знака самолетов не существует.
Плоскость можно задать двумя пересекающимися прямыми, тогда точкой пересечения прямых будет служить одна точка, а на одной и второй прямой — две произвольные точки.
Другой вид этой задачи — прямая линия и точка, не лежащая на этой прямой. По аналогии со вторым вариантом: одна точка уже существует и не лежит на прямой, а две другие — произвольные точки на существующей прямой.
Взаимное расположение прямой и плоскости
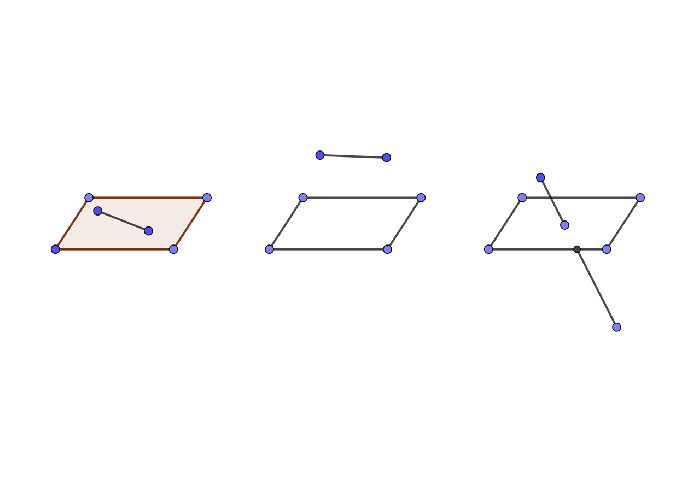
Прямая в пространстве может быть параллельна плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
Прямая параллельная плоскость, если она не имеет с ней общих точек. Признак параллельности прямой и плоскости чрезвычайно прост: прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости.
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, надо проехать прямо в плоскости через точку пересечения. Тогда угол между этими прямыми будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Знак перпендикулярности прямой и плоской поверхности следующий: прямая, перпендикулярная плоской поверхности, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоской поверхности и пересекает плоскую поверхность в месте пересечения этих прямые линии.
Прямая в пространстве может лежать в плоскости, если любые две точки прямой принадлежат плоскости.
Взаимное расположение плоскостей
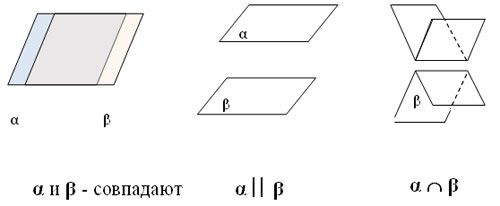
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если две пересекающиеся прямые попарно параллельны в каждой из плоскостей.
Плоскости могут пересекаться только по вертикали. В этом случае плоскости образуют угол. Чтобы найти его числовые значения, необходимо в каждой из плоскостей провести прямой перпендикуляр прямое пересечение плоскостей. Эти две прямые образуют плоский угол. Эти свойства иногда называют правилами плоскости.
Что мы узнали?
Мы дали определение и привели примеры плоскостности. Выделили вариации пресецения прямой и плосности и пересечения плосностей. Они привели несколько примет, связанных с самолетами, и проанализировали все случаи существования самолетов в космосе.








Комментирование закрыто