
Начиная с 5-го класса учащиеся начинают знакомиться с понятием площадей различных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из самых простых для изучения.
Понятия площади
Любая фигура имеет свою площадь, и расчет площади ведется на основе единичного квадрата, то есть квадрата с длиной стороны 1 мм, или 1 см, 1 дм и так далее. Площадь такой фигуры равна $1*1 = 1мм^2$ или $1см^2$ и т д. Площадь обычно обозначают буквой S.
Площадь показывает размер части плоскости, занимаемой фигурой, очерченной отрезками.
Прямоугольник – это квадрат, у которого все углы имеют одинаковую градусную меру и равны 90 градусам, а противоположные стороны попарно параллельны и равны.
Особое внимание нужно обращать на единицы измерения длины и ширины. Они должны совпадать. Если единицы не совпадают, их переводят. Как правило переводят большую единицу в меньшую, например, если длина дается в дм, а ширина в см, то дм переводят в см, а результат получится в $см^2$.
Формула площади прямоугольника
Чтобы найти площадь прямоугольника без формулы, посчитайте количество единичных квадратов, на которые разделена фигура.

Прямоугольник разделен на 15 квадратов, т.е площадь равна 15 см2. Стоит отметить, что фигура занимает 3 квадрата в ширину и 5 в длину, поэтому для расчета количества единичных квадратов нужно длину умножить на ширину. Чем меньше ширина стороны квадрата, тем больше длина. Таким образом мы можем вывести формулу площади прямоугольника:
S = a · b, где a,b — ширина и длина фигуры.
Например, если длина прямоугольника 5 см, а ширина 4 см, площадь будет 4*5 = 20 см2.
Расчет площади прямоугольника, с использованием его диагонали
Чтобы вычислить площадь прямоугольника по диагонали, нужно воспользоваться формулой:
$$S = {1\over{2}} ⋅ d^2 ⋅ sin{α}$
Если в задаче дано значение угла между диагоналями, а также значение самой диагонали, то площадь прямоугольника можно вычислить по общей формуле для произвольных выпуклых квадратов.
Диагональ – это отрезок, соединяющий противоположные точки фигуры. Диагонали прямоугольника равны, а точка пересечения делится пополам.
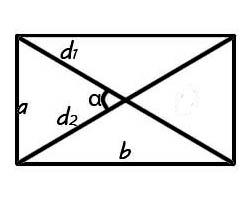
Примеры
Для закрепления темы рассмотрим примеры заданий:
Нет. 1. Найдите площадь садового участка такой же формы, как на рисунке.
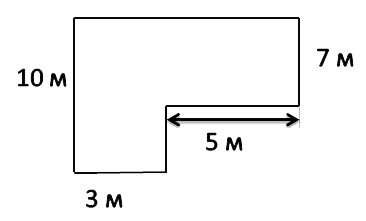
Решение:
Чтобы вычесть площадь, разделите фигуру на два прямоугольника. Один из них будет иметь размеры 10 м и 3 м, другой 5 м и 7 м. Отдельно находим их площади:
$S_1 =3*10=30 м^2$;
$S_2=5*7=35м^2$.
Затем нужно найти их сумму:
$30+35=65 м^2$
Это будет площадь садового участка $S = 65 м^2$.
Нет. 2. Вычислите площадь прямоугольника, если диагональ d=6 см и угол между диагоналями α =300.
Решение:
Значение $sin 30 ={1\over{2}} $,
$ S ={1\over{2}}⋅ d^2 ⋅ sinα$
$S ={1\более{2}} * 6^2 * {1\более{2}} =9 см^2$
Таким образом, $S=9 см^2$.
Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не являются биссектрисами углов прямоугольника. А еще если нарисовать биссектрисы каждого угла, то при их пересечении получится прямоугольник.
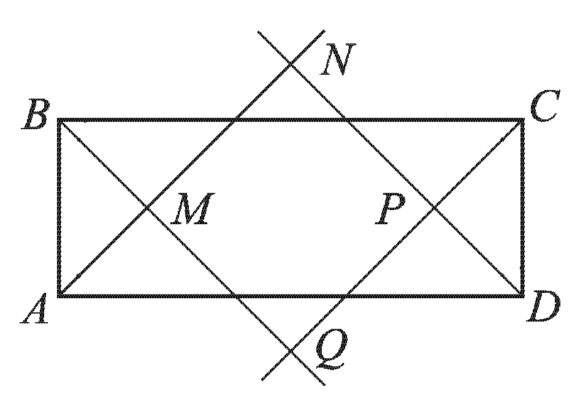
Что мы узнали?
Мы узнали, как найти площадь прямоугольника. В зависимости от исходных данных используется определенная формула для нахождения площади. Не забывайте, что если в задании указаны разные единицы измерения сторон, необходимо преобразовать одну из них.








Комментирование закрыто