
Все с начальной школы знают формулу площади прямоугольника. Площадь прямоугольника равна произведению его длины и ширины. Но иногда бывает, что длину или ширину узнать не удается, а значения диагоналей есть.
Определения
Давайте поговорим о нескольких определениях, которые необходимы для понимания этой темы.
Прямоугольник – это выпуклый квадрат, стороны которого попарно равны и параллельны, а углы равны 90 градусов. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны.
Что такое диагональ? Диагональ – это отрезок, соединяющий противоположные стороны фигуры. Диагональ встречается во всех фигурах, число вершин которых больше 3. У треугольника диагоналей нет, а у тетраэдра или додекаэдра они есть.
Четырехугольники подразделяются на выпуклые и невыпуклые. Выпуклые четырех угольники определяют по следующему правилу: через любые две соседние вершины фигуры проводят прямую. Если фигура лежит по одну сторону от прямой, то четырехугольник выпуклый, если нет – невыпуклый. Все известные четырехугольники являются выпуклыми.
Формула площади прямоугольника
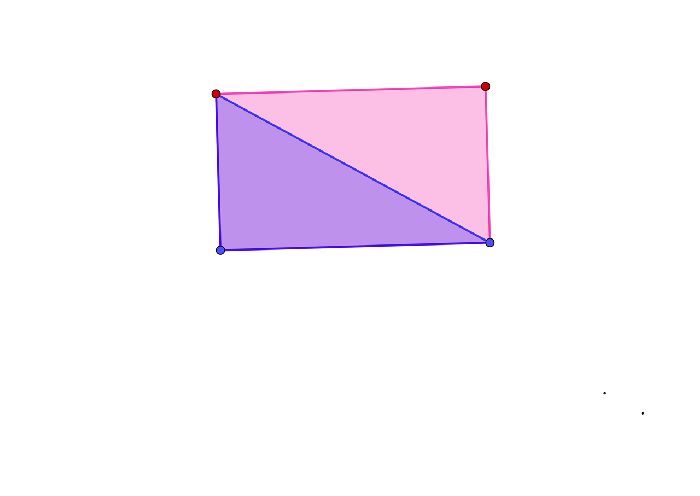
Площадь прямоугольника обычно определяют как произведение его длины и ширины. Эта формула получается путем деления фигуры по диагонали на два прямоугольных треугольника. Площадь каждой фигуры равна половине произведения ног. Суммарная площадь двух фигур равна всему произведению ног. Эти ножки точно равны длине и ширине прямоугольника.
Но бывают ситуации, когда нужно поискать местность, а значений долготы и широты нет. Что делать тогда? Воспользуйтесь формулой, общей для всех четырех прямоугольников, и найдите площадь прямоугольника, используя диагонали.
Площадь любого выпуклого четырехугольника равна произведению диагоналей на синус угла между ними. Диагонали прямоугольного треугольника равны между собой, поэтому угла и диагонали достаточно, чтобы найти площадь.
$$S={1\over2}*d^2*sin(a)$
Внимательно следите за тем, какой именно угол дан в условиях задачи. Необходим острый угол при диагоналях. Если тупой, то можно воспользоваться формулой смежного угла. Если дан какой-либо из углов между стороной и диагональю, то придется искать другие пути решения.
Могут возникнуть ситуации, когда нужно найти площадь, но известен угол между диагональю и стороной и значение диагонали и стороны. Затем нужно найти площадь прямоугольного треугольника по формуле с использованием синуса и удвоить ее.
В этом случае площадь прямоугольника будет равна:
S=d*b*sin(а)
Что мы узнали?
Мы говорили о площади прямоугольного треугольника. Мы отдельно выделили формулу площади прямоугольника через диагонали. Мы рассказали о случаях, когда использование этой формулы невозможно или затруднено и дали альтернативное решение.








Комментирование закрыто