
В школьном курсе математики для 4-5 классов рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.
Определение понятия
Площадь указывает размер плоскости, которую занимает фигура. Если вырезать из листа бумаги фигуру, поместить ее на поверхность, а затем обвести ее карандашом, мы получим наглядное представление о свойствах площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Характеристики понятия
Район имеет несколько особенностей:
- Позитивность. Площадь не может быть отрицательной, как и пространство не может быть отрицательным. Есть только один случай, когда площадь стремится к нулю: измерение площади точки.
- Нормализация. Что это значит? Это значит, что у площади есть некий эталон, с которым сравнивают поверхность любой фигуры. Стандартом площади является квадрат со сторонами 1 х 1. Если это квадрат со сторонами 1 х 1 см, то единицей измерения площади будет см в квадрате и т д.
- Если две фигуры соединить так, что у них нет общих внутренних точек, то есть совместить фигуры по какой-либо стороне, то площадь получившейся фигуры будет равна сумме площадей двух исходных фигур.
На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.
Площади простых фигур
Формула определения площади зависит от фигуры. Обозначение местности чаще всего остается неизменным – это латинская заглавная буква «S». Это не правило, а всего лишь одна из традиций обозначения территории. В высшей математике, теплотехнике и многих других дисциплинах область может обозначаться и другими буквами.
Рассмотрим наиболее популярные формулы определения площадей:
- Прямоугольник. S=a*b – произведение длины и ширины.
- Треугольник. $S={1\over2}a*h$ — это половина произведения основания на высоту, проведенную к этому основанию.
- Круг. $S=\pi*r^2$ – отдельно следует отметить, что круг не может иметь площадь. Просто круг.
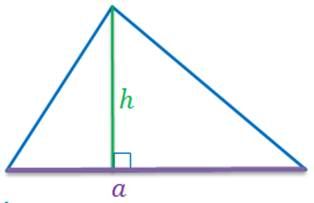
Сначала убедитесь, что параметры фигуры указаны в одних единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.
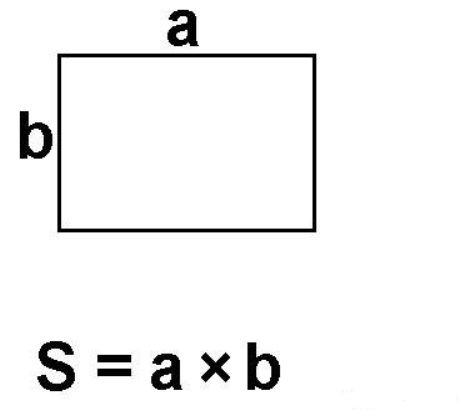
Какова площадь квадрата? Это сторона фигуры в квадрате. Потому что квадрат — это прямоугольник, длина и ширина которого равны:
$$S=а^2$
Если квадрат имеет сторону, равную 100 м, то его площадь равна одному гектару. Эту единицу применяют, когда необходимо оценить размер земельной поверхности при распределении земель сельскохозяйственного назначения:
$$1га=100м∙100м=10000м^2$
Площади полей можно измерять и в арах, которые в народе называют «сотками», поскольку одно представляет собой квадрат, сторона которого равна 10 м, а площадь эквивалентна 100 $м^2$.
$$1 год=100 млн^2$.
Площадь произвольной фигуры
Площадь сложной фигуры можно определить путем суммирования площадей частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадраты.
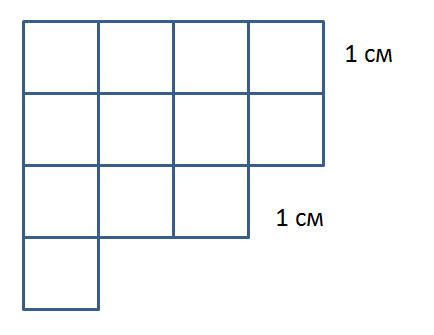
Фигуру на рисунке 3 можно разделить на 12 квадратов со сторонами 1 см. Тогда площадь каждого квадрата будет равна $1см^2$. Получается, что площадь рассматриваемой фигуры составит $12 см^2$.
Что мы узнали?
Мы познакомились с понятием площади. Мы узнали, что у каждой фигуры свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.








Комментирование закрыто