Площадь поверхности кубоида

В курсе математики 5 класса изучается тема прямоугольный параллелепипед. Сегодня мы поговорим о формулах нахождения площади боковой поверхности и полной площади поверхности этой фигуры, которые чаще всего вызывают затруднения у учащихся.

Определения

Параллелепипед – это фигура в пространстве, состоящая из шести квадратов.

Каждый квадрат представляет собой грань параллелепипеда. Среди граней четыре боковых и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется кубоидом.

Стороны граней являются ребрами. У параллелепипеда всего 12 ребер.

У параллелепипеда 8 вершин; Для их обозначения используются заглавные буквы.

Если две грани не имеют общего края, их называют противоположными. Поскольку каждая сторона кубоида представляет собой прямоугольник, противоположные стороны которого равны, то противоположные стороны кубоида также равны.

Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.

Площадь поверхности кубоида

Рис. 1. Прямоугольный параллелепипед

Мы часто встречаем в своей жизни примеры таких фигур: кирпич, коробка, системный блок компьютера.

Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.

Существует несколько типов параллелепипедов, имеющих основание в виде квадрата, параллелограмма или прямоугольника.

Формула для нахождения площади

Чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить площадь каждой боковой поверхности отдельно и затем просуммировать полученные значения.

$S = аб$;

$S = ак$; где а, b, с — стороны фигуры.

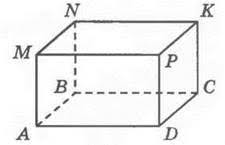
Площадь поверхности кубоида

Рис. 2. Прямоугольный параллелепипед

А поскольку противоположные поверхности равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, то их сумма и будет площадью боковой поверхности многоугольника.

$S= 2(ab + ac)$

Следовательно, чтобы вычислить общую площадь поверхности прямоугольного параллелепипеда, необходимо сложить площадь боковой поверхности и две площади основания. В результате получается формула площади прямоугольного параллелепипеда.

$S = 2(ab + ac) + 2bc = 2(ab + ac + bc)$

Иногда для наглядности рядом со знаком площади пишут краткое обозначение, например S с – общая площадь поверхности, или S б п – боковая поверхность. Это помогает не перепутать необходимые данные во время выполнения задачи.

Пример задания

Найдите полную площадь поверхности прямоугольного параллелепипеда, если длина и ширина основания равны 4 см и 3 см соответственно, а высота 2 см.

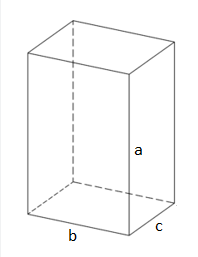
Площадь поверхности кубоида

Рис. 3. Прямоугольный параллелепипед со сторонами a, b, c

Решение:

S пп = 2(ab + ac + bc)

S пп = 2(4*3 + 4*2 + 3*2) = 52 см2

Таким образом, S пп = 52 см2.

Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.

Что мы узнали?

Мы познакомились с элементами прямоугольного параллелепипеда: гранями, ребрами, основанием. Также нас познакомили с формулами нахождения площади его боковой и полной поверхности, которые можно использовать для решения задач.