Периметр равностороннего треугольника

Равносторонний треугольник занимает особое место среди треугольников. Чтобы найти значение периметра, площади, углов или радиусов вписанной и описанной окружностей равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой — авторы задач редко разбираются в странице и им приходится искать решения.

Формула нахождения периметра равностороннего треугольника

Формула периметра равностороннего треугольника следует из определений. Что такое окружность? Периметр – это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, стороны которого равны.

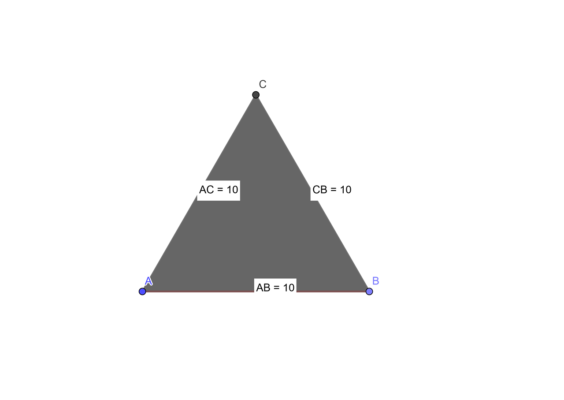
Это значит, что чтобы найти значение периметра, достаточно размер страницы умножить на количество страниц:

Р=3*а

Давайте решим несколько задач разной сложности, чтобы узнать, какие проблемы могут возникнуть на пути нахождения периметра.

Задача 1

Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Эта задача не должна быть сложной:

Р=3*а=3*6=18

Задача 2

В этом упражнении дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник также является равносторонним.

Учтем размер угла. Угол при основании равен 60. Также углы при основании равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Это означает, что в основании есть два угла по 60 градусов. Рассчитаем угол при вершине:

180-60-60=60 – угол вверху тоже 60 градусов.

Это означает, что этот треугольник будет равносторонним, так как все углы равны 60 градусам.

Существует отдельная формула площади равностороннего треугольника:

$$S=a^2*{\sqrt{3}\over 4}={64\over\sqrt{3}}$$ – где a – значение стороны, которую нам нужно выразить из этой формулы.

$$а^2={S\over{\sqrt{3}\over 4}}$

$$a^2={4S\over\sqrt{3}}$

$$a=\sqrt{4S\over\sqrt{3}}$

$$a={\sqrt{4*{64\over\sqrt{3}^2}}\over\sqrt{3}}=\sqrt{4*64}=16$

Подставим полученное значение в формулу:

Р=3*а=3*16=48

Задача 3

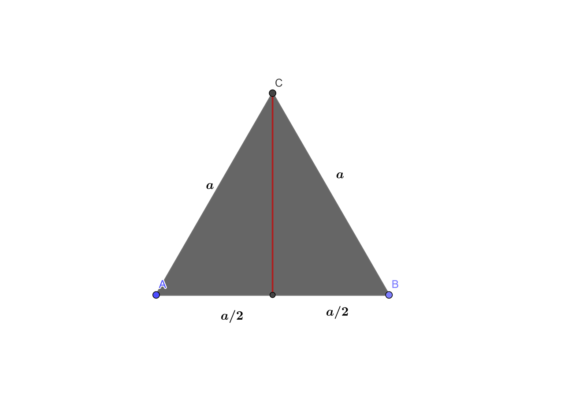
Для этой задачи вам нужно использовать метод решения, часто используемый в задачах о равнобедренном треугольнике. Из любой вершины опускаем высоту, которая будет медианой и биссектрисой.

В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:

$$h^2=a^2-({a\over2})^2$

$$h^2=a^2-{a^2\over4}$

Вычтем подобные члены:

$$h^2={3\over4}*a^2$

Из полученной формулы выражаем ценность страницы:

$$a^2={4\over3}*h^2$

$$a=\sqrt{{4\over3}*h^2}$

$$a=\sqrt{{4\over3}*(3*\sqrt{3})^2}$

$$a=\sqrt{{4\over3}*(9*3)}$

$$a=\sqrt{4*9}$

а=6

Подставим полученное значение в формулу периметра равностороннего треугольника.

Р=3*а=3*6=18