
Правильный треугольник особенно выделяется на фоне других фигур. Любой параметр в таком треугольнике можно определить по длине стороны. Найти окружность особенно легко.
Определения
Для начала напомним некоторые определения, которые понадобятся для решения задач на нахождение периметра правильного треугольника:
- Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам.
- Правильный треугольник — это частный случай равнобедренного треугольника, поэтому любая высота в правильном треугольнике будет биссектрисой и медианой.
- Некоторые формулы для произвольного треугольника, примененные к правильному треугольнику, можно значительно упростить, используя теорему Пифагора.
Периметр треугольника
Что такое окружность? Это сумма длин всех сторон.
Формула периметра одинакова для любой фигуры. Это всегда сумма длин всех сторон.
Особенно для правильного треугольника помните, что все стороны этой фигуры равны между собой. У треугольника 3 стороны, а это значит, что формула периметра следующая:
$$P=3a$
Пример
Нелегко придумать сложную задачу нахождения периметра равностороннего треугольника. Поэтому мы решим интересную, но простую задачу по заданной теме. В процессе решения мы рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.
Площадь правильного треугольника ABC равна $9\sqrt{3}$
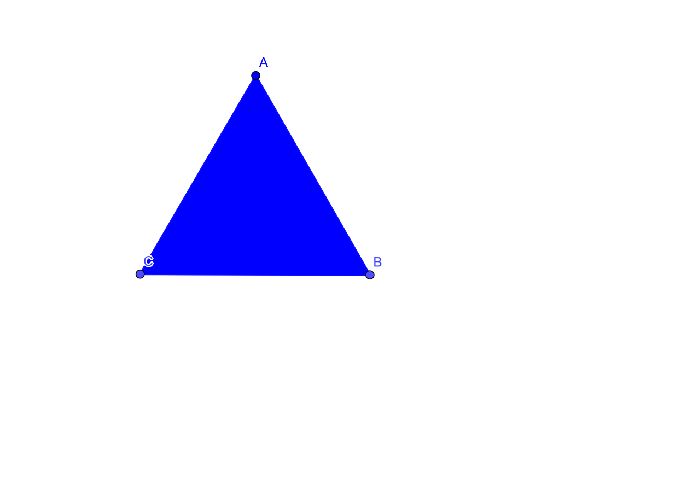
Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин. Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи.
Давайте вспомним формулу площади треугольника и упростим ее для равностороннего треугольника.
Площадь треугольника находится как половина произведения основания на высоту, проведенную к основанию.
В правильном треугольнике ABC проведем медиану AM, совпадающую с высотой и биссектрисой. Тогда треугольник АВМ будет прямоугольным. Используя теорему Пифагора, находим AM.
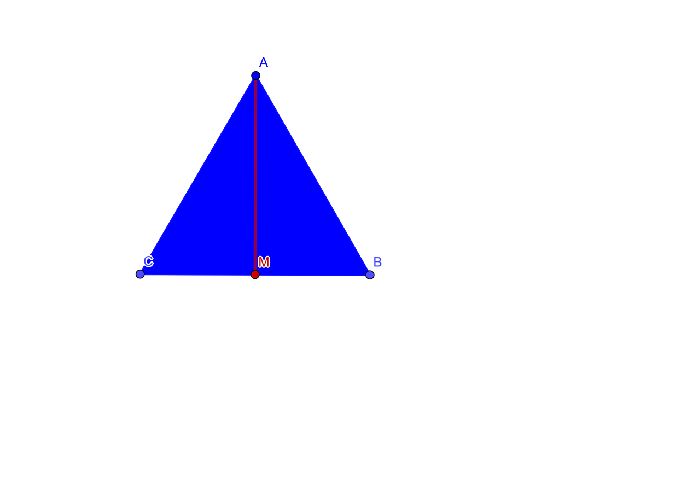
$$AM=\sqrt{AB^2-BM^2}= \sqrt{a^2-{a\over{2}}^2}= \sqrt{a^2-{{a^2}\over {4}}}=\sqrt{{3a^2}\over{4}}$
Подставим значение АМ в формулу площади:
$$S={1\over{2}}*a*h={1\over{2}}*a*a*{\sqrt{3}\over{2}}=a^2*{\sqrt {3}\более{4}}$
Из этой формулы выражаем ценность страницы:
$$a=\sqrt{4S\over{\sqrt{3}}}=\sqrt{{4*{9\over{\sqrt{3}}}}\over{\sqrt{3}}}=6$
Теперь найти периметр не будет проблемой.
$$P=3a=3*6=18$
Что мы узнали?
Мы дали формулу периметра правильного треугольника. На примере они показали, как можно найти площадь правильного треугольника с помощью площади. На том же примере они показали приблизительную прогрессию решения любой задачи на решение правильного треугольника.








Комментирование закрыто