
Прямоугольный треугольник содержит огромный набор зависимостей. Это делает его привлекательным объектом для решения различных геометрических задач. Нахождение гипотенузы считается одной из наиболее часто встречающихся задач.
Прямоугольный треугольник
Прямоугольный треугольник – это треугольник, коротать в прямом себе угол, т.е угол в 90 градусов. Только в прямоугольном треугольнике можно выразить тригонометрические функции через величины сторон. В произвольном треугольнике необходимо произвести дополнительные конструкции.
В прямоугольном треугольнике две высоты из трех совпадают со сторонами и называются катетами. Третья сторона называется гипотенузой. Высота, проведенная гипотенузе, уникальна для треугольников этого типа и требует дополнительных построений.
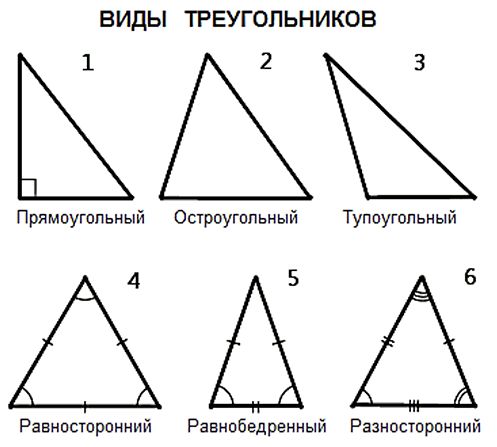
В прямоугольном треугольнике не может быть тупых углов. Так же, как невозможно и существование второго прямого угла. В этом случае нарушается тождество суммы углов треугольника, которая всегда равна 180 градусам.
Гипотенуза
Перейдем непосредственно к гипотенузе треугольника. Гипотенуза – это самая большая сторона треугольника. Гипотенуза всегда больше любого из катетов, но при этом сумма катетов всегда меньше. Это следствие теоремы о неравенстве треугольника.
Теорема гласит: в треугольнике ни одна сторона не может добавить больше двух других. Существует и вторая формулировка или вторая часть теоремы: в треугольнике, наоборот, большая сторона лежит на большем углу, и наоборот.
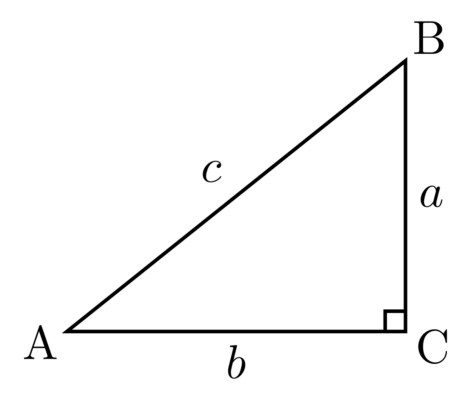
В прямоугольном треугольнике большой угол является прямым, так как не может быть второго прямого угла или тупого угла по уже упомянутым причинам. Такая натрадная программа угла всегда легит большую строку.
Кажется непонятным, почему именно прямоугольный треугольник заслужил отдельное наименование каждой из сторон. На самом деле, в равнобедренном треугольнике стороны так же носят свои названия: боковые стороны и основание. Но именно за катеты и гипотенузы учителя особенно любят ставить двойки. Почему? С одной стороны это дань памяти древним грекам, изобретателям математики. Именно они изучали прямоугольные треугольники и наряду с этими знаниями оставили целый пласт информации, на котором строится современная наука. С другой же стороны существование этих названий значительно упрощает формулировки теорем и тригонометрических тождеств.
Теорема Пифагора
Если учитель спрашивает о формуле гипотенузы прямоугольного треугольника, то с вероятностью 90% он имеет в виду теорему Пифагора. Теорема гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратных катетов.
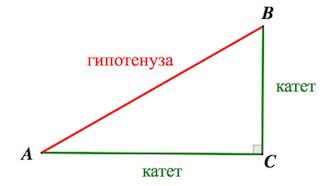
Обратите внимание, насколько точно и полно сформулирована теорема. Подробные простоты имного простого без очень гипотетических контактов и катеты.
Теорема имеет следующую формулу:
$c^2=b^2+a^2$ – где с – гипотенуза, a и b – катеты прямоугольного треугольника.
Что мы узнали?
Мы говорили о том, что такое прямоугольный треугольник. Узнали, зачем придумали общие названия катетов и гипотенузы. Они объяснили некоторые свойства гипотенузы и вывели формулу длины гипотенузы треугольника с помощью теоремы Пифагора.








Комментирование закрыто