
В школьном курсе математики прямоугольник является одной из первых фигур, которые изучают.Диагональ прямоугольника участвует в решении многих задач. Поэтому имеет смысл присмотреться к этому элементу на рисунке.
Определение
Прямоугольник – это квадрат с равными углами и парами равных и параллельных противоположных сторон.
Следовательно, диагональ разделит данную геометрическую фигуру на два прямоугольных треугольника. Оказывается, значение этого отрезка можно найти через квадратный корень из суммы квадратов соответствующих сторон прямоугольника (согласно теореме Пифагора).
Диагональ прямоугольника обозначается маленьким латинским символом d или двумя заглавными буквами после названий вершин, которые соединяет диагональ.
Длина диагонали прямоугольника, вокруг которого описана окружность, равняется диаметру этой окружности.
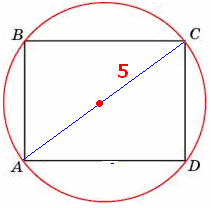
Это свойство может помочь решить задачи по нахождению сторон треугольника.
Характеристики понятия
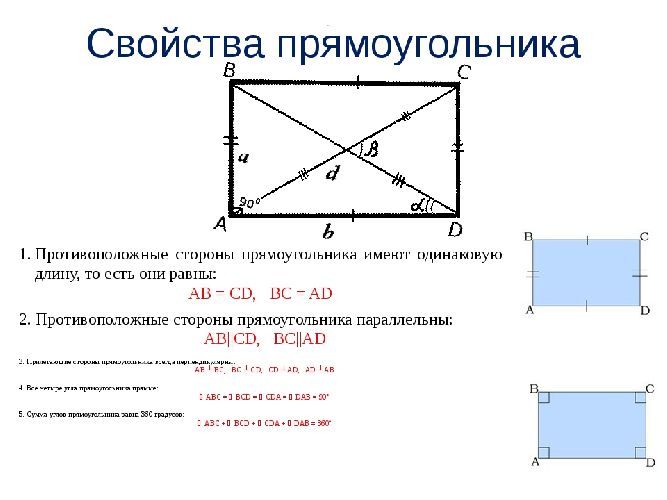
Диагональю прямоугольника называется отрезок, соединяющий углы прямоугольника, противоположные друг другу. Соответствующий параметр можно найти, используя периметр основной геометрической фигуры, ее площадь или соотношение соответствующих сторон. Для этого воспользуемся формулой диагонали прямоугольника:
$d=\sqrt{a^2+b^2}$, где a и b — стороны прямоугольника.
Значение
В математике выделяют свойства диагоналей прямоугольника. Таким образом, эти отрезки пересекаются в одной точке и делятся пополам точкой пересечения. В прямоугольнике диагонали будут равны.
На этом рисунке наглядно показаны углы, образующие диагонали.
Если диагонали параллелограмма равны, то эта геометрическая фигура является прямоугольником. Можно утверждать то же самое, когда сумма квадратов отрезков параллелограмма равна квадрату его диагонали (естественно речь идет о теореме Пифагора).
Что мы узнали?
Свойства диагонали прямоугольника используются для нахождения важных параметров этой фигуры. При решении задач, где необходимо доказать существование квадрата определенного типа, часто рассматривают диагонали параллелограмма. С помощью этих отрезков можно найти площадь фигуры, которой они принадлежат.








Комментирование закрыто