
Шестнадцатеричная система счисления используется для записи адресов и содержимого ячеек памяти компьютера. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение над ними арифметических действий имеет ряд функций, о которых вы можете прочитать в этой статье.
Что такое шестнадцатеричная система счисления
Шестнадцатеричная система счисления использует шестнадцать символов для записи числовых значений: арабские цифры от 0 до 9 и латинские буквы A, B, C, D, E, F. Соответственно, основой такой системы счисления будет число 16.
При использовании шестнадцатеричных чисел следует помнить, что в числовом ряду шестнадцатеричных чисел после числа 9 идет А, а после F следует двузначное число 10.
Перевод 16 –10
Для перевода шестнадцатеричного числа непосредственно в десятичную систему удобно использовать расширенную форму записи, когда число представляется в виде суммы, в которой слагаемые получаются умножением знака места (числа или числового эквивалента числа) буква) на 16 в силе соответствующего места.
Например, 1F4 = 1 * (16^2) + 15 * (16^1) + 4 * (16^0) = 256 + 240 + 4 = 500
Обратный перевод осуществляется путем последовательного деления десятичного числа на 16 и взятия остатка от деления. Также полученные остатки в диапазоне от 10 до 15 необходимо заменить на соответствующую букву.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500/16 = 31 (остаток 4)
31/16 = 1 (оставшиеся 15 заменить на букву F)
Таким образом получается шестнадцатеричное число 1F4.
Перевод 16 – 2
Чтобы преобразовать шестнадцатеричное число в десятичную систему, каждая цифра заменяется группой из четырех нулей и единиц, обычно называемой «тетрадой». Для перевода обычно используется таблица соответствия между шестнадцатеричными символами и двоичными тетрадами.
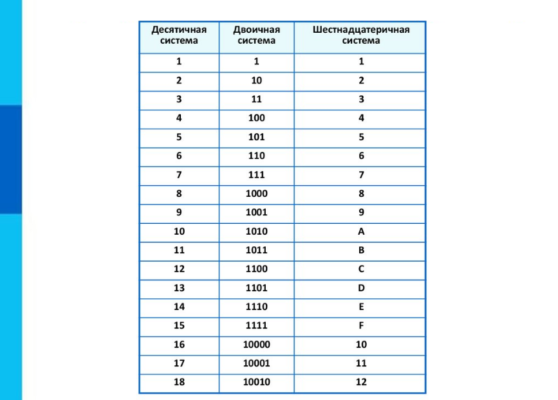
Например, 1F4 = (0001)(1111)(0100).
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с помощью шестнадцатеричной таблицы сложения. А сложение или вычитание производится поразрядно, начиная с младшей цифры.

Если при сложении двух чисел с одинаковой цифрой получается двузначное число, то к старшей цифре прибавляется значение его старшей цифры (единицы.
Например, 1F + 2D = 4C.
Сначала значения младших цифр F+D складываются. Из таблицы получается двузначное число 1С, куда переносится единица старшей цифры и прибавляется к сумме вторых по величине цифр в добавляемых шестнадцатеричных числах.
Сумма цифр старших цифр 1+2 равна 3 и прибавляется переносная единица, то есть сумма равна 4.
Это дает число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо заимствовать от старшей цифры, если уменьшаемое конкретной цифры меньше вычитаемой. Затем в бой вступает отряд более высокого ранга. Значение дифференциала показано в таблице.
Например, 2D – 1F = E.
Сначала найдите разницу между цифрами младших разрядов, то есть D – F (в десятичной записи 13-15). Исключаемое меньше вычитаемого, поэтому единица заимствована из старшей цифры исходного числа. То есть вычисляется разница 1D – F = E.
После того как манипуляции с младшими цифрами завершены, переходят к следующим по величине. В данном примере следует посчитать 2 – 1. Но ранее единица была заимствована, и в старшей цифре при уменьшаемом осталась не 2, а 1. Поэтому вычисляется разница 1 – 1 = 0.
Умножение и деление
Также следует поразрядно умножать и делить числа в шестнадцатеричной системе. При выполнении вычислений удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
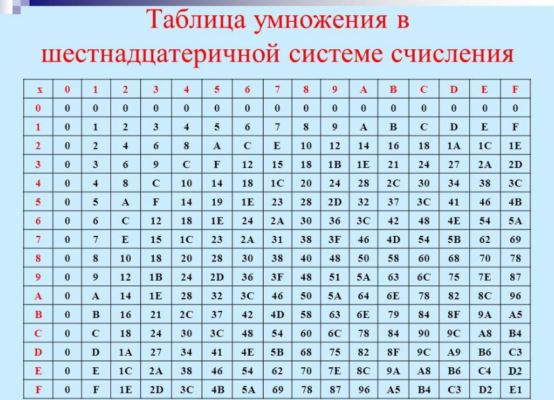
Например, 1С*2=38. Используя распределительный закон умножения: (10+С)*2=10*2+С*2=20+18=38
Операцию деления производят также в столбце с помощью таблицы умножения: 1С/2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этого строка и столбец, где находится 1С, дадут значение частного числа деления, то есть Е.
Что мы узнали?
Шестнадцатеричная система счисления использует цифры от 0 до 9 и латинские буквы от A до F для записи числовых значений. Непосредственное преобразование шестнадцатеричного числа в десятичную систему осуществляется с помощью расширенной формы записи числа. Обратный перевод осуществляется путем деления и записи остатка. Каждую шестнадцатеричную цифру числа можно заменить тетрадой двоичных чисел. Арифметические действия в шестнадцатеричной системе удобнее всего выполнять поразрядно, используя шестнадцатеричные таблицы сложения и умножения








Комментирование закрыто