
Одним из инструментов имитационного моделирования является метод решения задач с помощью эксперимента со случайными числами, который называется методом Монте-Карло. Область применения этого метода и его алгоритм описаны в этой статье.
Что такое метод Монте-Карло
Метод Монте-Карло относится к группе численных методов решения задач, в которых присутствует элемент неопределенности. Он позволяет получать приблизительные результаты на наборе входных значений, которые выбираются случайным образом путем генерации случайных чисел.
Название этого метода выбрано в честь города Монте-Карло, известного своими казино. Рулетка в казино – это своего рода генератор случайных чисел. Этот метод впервые был описан в 1949 году в совместной работе математиков Николаса Метрополиса и Станислава Улама. Известно, что название придумал Н. Метрополис в честь одного из своих родственников, который был азартным игроком и частым посетителем казино.

Использование метода Монте Карло для вычисления площади фигуры
Простым примером, иллюстрирующим применение этого метода, является метод определения площади фигуры сложной формы, когда контуры предмета не образуют геометрическую фигуру, для расчета которой имеется готовая формула.

Для вычисления площади S такой фигуры ее вписывают в квадрат со стороной а. Точки внутри квадрата затем выбираются случайным образом. При этом точки могут попадать как внутри изучаемой фигуры сложной формы, так и за ее пределы.
Чем большую площадь занимает фигура внутри квадрата, тем чаще в него будут попадать очки. Точки, попадающие внутрь фигуры, отмечены буквой м, а все выделенные точки внутри квадрата отмечены буквой н.
Здесь вырисовывается закономерность: чем больше точек участвует в эксперименте, тем больше вероятность того, что процент точек в исследуемой фигуре стремится к отношению площади фигуры к площади квадрата. Математически это можно записать так: s=a*a*(m/n).
Таким образом, достигнут определенный метод определения площади фигуры произвольной формы методом статистического испытания. Модели расчета площади разных фигур сложной формы, сформированные таким образом, будут различаться математическими описаниями фигур.
В теории вероятностей и математической статистике действует закон больших чисел, согласно которому результат эксперимента окажется свободным от случайных воздействий только в случае большого количества случайных факторов, то есть будет прослеживаться устойчивая закономерность. Проще говоря, чем больше число испытаний, тем точнее будет результат.
Алгоритм вычисления площади фигуры с помощью метода Монте Карло
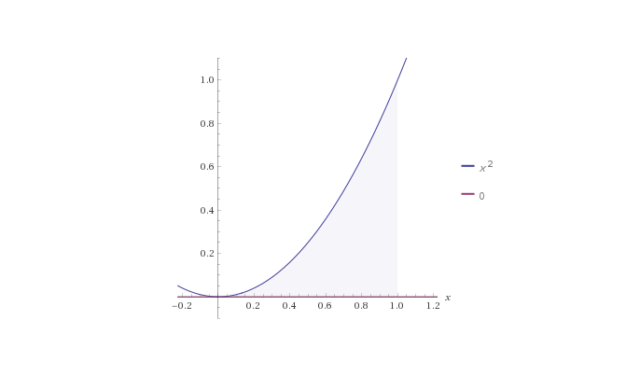
Определим площадь фигуры, ограниченной уравнениями y = x^2, y = 0 и x = 1.
Сделаем модель: площадь нужной фигуры укладывается в квадрат. Если значения координат x и y принадлежат диапазону [0;1], то точка принадлежит квадрату. Если выполняется система неравенств 0 < x < 1 и 0 < y – x^2, то точка принадлежит фигуре.
Поскольку длина стороны квадрата равна 1, площадь фигуры после подсчета количества точек будет определяться по формуле: s=m/n
Алгоритм решения задачи будет выглядеть следующим образом:
- Задайте n (решите, сколько попыток должно быть в задании)
- m=0 (начальное значение точек, попадающих в область фигуры. Переменная m будет служить счетчиком в алгоритме)
- Введите значение x, генерируя случайные числа
- Установите значение y, генерируя случайные числа
- Организовать повторение цикла (перебирает целочисленные значения от 0 до девяти шагов по 1). Тело цикла:
- условие проверки 0 < x < 1, если true, продолжайте проверять второе условие, иначе увеличьте счетчик цикла на 1
- проверить условие 0 < y – x^2, если условие истинно, организовать команду счетчика точек (m=m+1), в противном случае счетчик цикла увеличивается на 1
- с=м/н
- Распечатать результат p
Что мы узнали?
Одним из способов построения моделей является метод статистического тестирования, называемый методом Монте-Карло. Важным условием использования статистических методов является проведение большого количества тестов путем генерации случайных входных параметров. Используя метод Монте-Карло, можно вычислить площадь фигуры любой формы.








Комментирование закрыто