
Математическая логика занимается изучением логических законов, используемых в теории множеств. Основы логической алгебры изучаются в курсе информатики в 8 классе. Над множествами можно выполнять различные операции, одна из которых — пересечение.
Пересечение множеств
Важным разделом информатики является алгебра логики. Знание логических законов и правил позволяет быстро решать сложные задачи в любой сфере деятельности – в юридических и экономических науках, в технике и технологии.
Множество чисел
Множество — это совокупность определенных и различных объектов, которые воспринимаются как единое целое.
Например, набор учеников в классе, набор натуральных чисел.
Множества могут быть конечными и бесконечными. Число учеников в классе — конечное множество; можно четко назвать конкретное количество студентов. Число положительных целых чисел бесконечно; оно может быть бесконечно большим.
В математике количество обозначается заглавными буквами.
Например, набор A={1,5,12,6,7} и набор B={2,4,12,3,7} являются конечными наборами натуральных чисел
С наборами можно выполнять различные действия. Одной из таких операций является пересечение наборов чисел.
Пересечение множеств чисел
С математической точки зрения пересечение двух множеств X и Y представляет собой третье множество Z, включающее элементы как из первого, так и из второго множества. Приведем примеры пересечения множеств чисел.
Для наборов чисел X={1, 2,4,5,6,8} и Y={2,3,4,6,7,9} пересечением будет третий набор Z={2, 4, 6}.
Элементами множеств могут выступать не только числа.
Для множеств A={A, B, C, D, D, E} и B={G, D, E, E, F} пересечением будет третий набор, элементами которого являются буквы, идентичные в исходных множествах C. = {Г, Д, Е}.
Обозначение пересечения
Операция пересечения называется и обозначается по-другому, но суть от этого не меняется. В теории множеств для обозначения точки пересечения используется знак ∩, и формула выглядит так: A ∩ B = C
Точку пересечения еще называют произведением величин, а для обозначения операции используют знак умножения: A ∙ B = C
В математической логике, работающей с высказываниями, используется термин «конъюнкция». Для его обозначения используют символ &: А&В=С. Допускается обозначать союз буквой И: А И В=С.
Визуальное представление пересечения
Для наглядного отображения операций с множествами используются диаграммы Эйлера, представляющие собой два круга, частично наложенных друг на друга. Видны круги. Заштрихованная область, одновременно принадлежащая каждому кругу, образованному перекрытием, является областью пересечения.
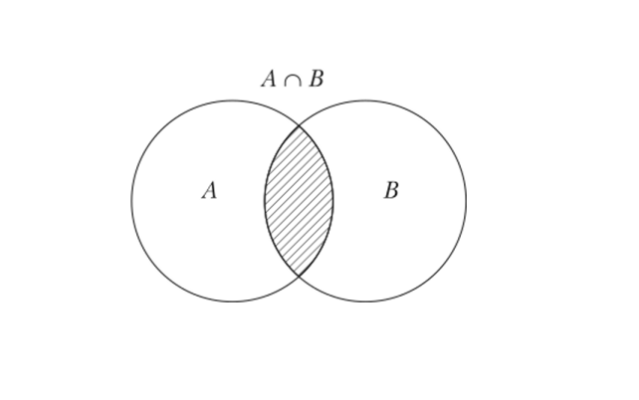
Круги Эйлера представляют собой простой инструмент, который доходчиво объясняет суть основ теории множеств. Широко известен цикл работ Леонарда Эйлера под названием «Письма к немецкой принцессе о разных физических и философских материях», написанный для дочерей маркграфа Бранденбург-Шведт. В письмах 102 – 104 второго тома этого произведения использован данный графический метод.

определение результатов операций над множествами с помощью кругов Эйлера упрощает решение логических задач.
Таблица истинности
В алгебре логики объектом, к которому применяются логические операции, является утверждение. Он представляет собой определенное повествовательное предложение, содержание которого можно однозначно определить как истинное или ложное. Если утверждение истинно, его обозначают единицей, если ложно, его обозначают нулем.
Например, утверждение «Москва – столица Российской Федерации» является верным утверждением. «Площадь квадрата равна сумме его сторон» — неверное утверждение.
Высказывание не может быть вопросительным или побудительным предложением, числовые выражения, которые не содержат логических операций, или содержащие переменные, также не являются высказываниями.
Таблицы истинности используются для указания всех возможных версий утверждений.
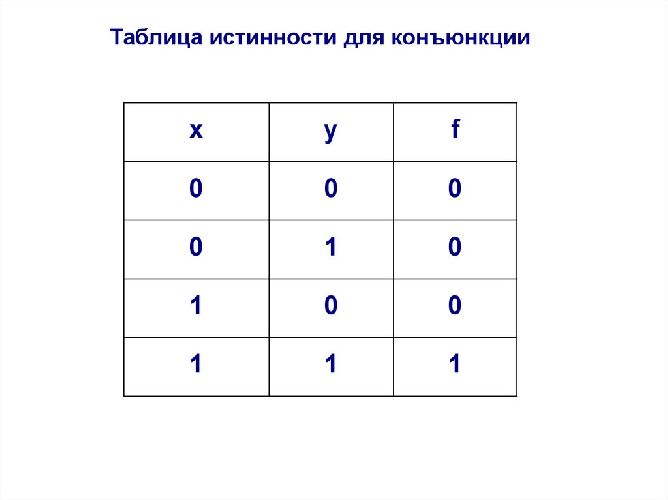
Из таблицы видно, что в результате операции конъюнкции (перекрестия) выражение истинно (равно 1) тогда и только тогда, когда оба исходных выражения истинны. Во всех остальных случаях результат равен нулю (ложь).
Что мы узнали?
Пересечение двух наборов представляет собой третий набор, содержащий элементы, общие для исходных наборов. Перекрестную операцию можно обозначать по-разному. Крест еще называют произведением количеств и соединения. Наглядно пересечение удобно представить с помощью диаграмм Эйлера. Таблицы истинности используются для отображения всех вариантов утверждений. Для пересечения результат истинен, только если оба операнда истинны.








Комментирование закрыто