
Все расчеты по математике производятся в позиционной десятичной системе счисления. Кратко о функциях десятичной системы вы можете прочитать в этой статье.
Что такое десятичная система счисления
В десятичной системе для обозначения чисел используются десять арабских цифр от 0 до 9; следовательно, основанием десятичной системы счисления является число 10.
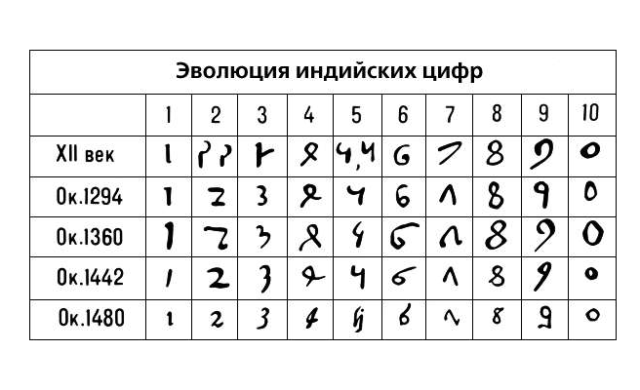
Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.
Развернутая форма представления десятичного числа
Важным понятием позиционного подхода к представлению чисел является понятие цифры. Есть единицы, цифры, десятки, сотни, тысячи и так далее. Любое десятичное число можно представить в так называемой расширенной форме, когда число записывается в виде суммы цифр, представленной как произведение значащей цифры в цифре и числа десять в степени соответствующей цифры.
Например, расширенное десятичное число 46758 будет выглядеть так:
46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0
Или вот так:
46758 = 4 * 10 000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1
Прямой перевод числа из десятичной системы
Преобразование целого десятичного числа в любую систему счисления производится путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится преобразование.
Например, чтобы преобразовать десятичное число в двоичное, разделите его на два, восьмеричное на восемь и шестнадцатеричное на шестнадцать. В принципе, десятичное число можно преобразовать как в пятеричную, так и в септальную систему путем деления на пять или семь.
После выполнения первого шага деления, скажем, на два, остаток запоминается, и полученное частное снова делится на базовое число. Эта операция выполняется до тех пор, пока последнее частное не станет меньше или равно делителю.
Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.
Например, прямой перевод числа 27 из десятичной системы в двоичную выполняется следующим образом:
27/2 = 13 и остаток 1
13/2 = 6 и остаток 1
6/2 = 3 и остаток 0
3/2 = 1 и остаток 1
Итак, 27 в двоичном формате равно 11011.
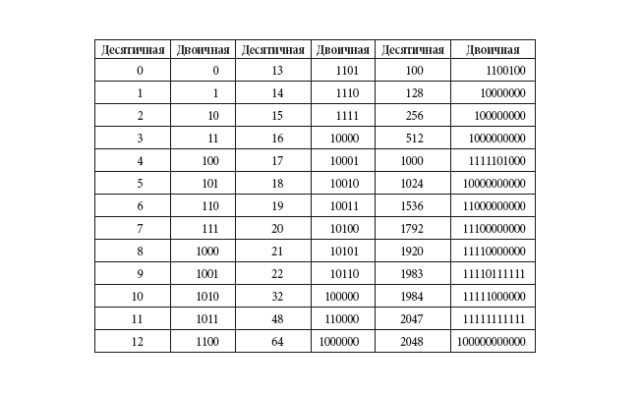
Для преобразования чисел внутри можно использовать таблицу соответствия между десятичными и двоичными числами
Обратный перевод числа в десятичную систему
Для перевода чисел в десятичную систему удобно использовать развернутую форму. При этом числовые значения записываются как сумма произведений цифр на цифры исходя из текущей системы счисления в степени цифры.
Например, двоичное число 11011 можно представить следующим образом:
1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 27
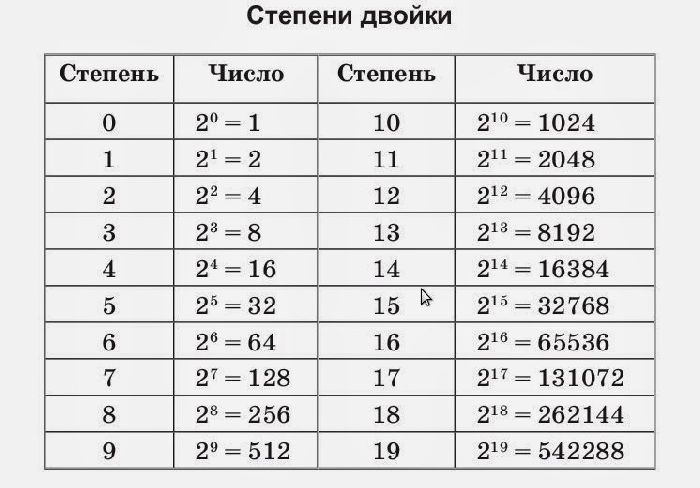
Для упрощения расчетов удобно использовать мощность двух таблиц
Что мы узнали?
В десятичной системе позиций используются десять арабских цифр для представления числовых значений. Числа в такой системе можно представить в расширенном виде. Преобразование десятичных чисел в другую систему осуществляется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять, используя развернутую форму для записи числа.








Комментирование закрыто