
Числа могут быть представлены не только в десятичном формате, но и в восьмеричной системе счисления, в которой для обозначения используются символы 0, 1, 2, 3, 4, 5, 6, 7. Как перевести числа в восьмеричную систему счисления из десятичной и двоичной систем и наоборот, описано в этой статье.
Восьмеричная система счисления
Восьмеричная система счисления имеет вспомогательный характер; удобно использовать для сокращения двоичных комбинаций чисел. Его удобнее использовать, чем двоичный, поскольку он использует меньше цифр. Восьмеричная система использовалась одно время для программирования на машинном языке, а также в устройствах подготовки данных, которые устарели с появлением персональных компьютеров.
Восьмеричный алфавит состоит из восьми цифр от 0 до 7 соответственно, основание — 8. Числовые ряды восьмеричных чисел: 1, 2, 3, 4, 5, 6, 7,10, 11, 12, 13, 14, 15, 16, 17, 20.
Следует обратить внимание, что после 7 в числовом ряду идет 10, а после 17 число 20.
Число 8 имеет символический смысл, является первым кубом двойки и отождествляется с трехмерным измерением. Для многих древних народов восьмёрка сакральное число. Внешне выглядит как символ бесконечности. В информатике один байт равен 8 битам.
Перевод 8 – 2
Преобразование восьмеричного числа в двоичное — самый простой способ преобразования чисел. Каждой восьмеричной цифре соответствует группа из трех двоичных цифр. Эта группа называется триадой.
И наоборот, когда вы конвертируете двоичное число в восьмеричный формат, три двоичных цифры заменяются одной восьмеричной. Деление целого двоичного числа на трёхзначные единицы производится справа налево. Когда крайняя тройка оказывается неполной, ее дополняют нулями.
Для более быстрого преобразования чисел используется таблица записи восьмеричных чисел в двоичный формат.

Например, 348 = 0111002. Перед числом ставим ноль и получаем 111002.
И обратный перевод, например: 11011012 = (001)(101)(101) = 1558. В старшей тройке не хватило цифр, она дополнялась слева двумя нулями.
Перевод 8 – 10
Преобразование чисел из восьмеричного формата в десятичный осуществляется с помощью правила перевода: целая часть числа делится последовательно на основание новой системы счисления, то есть 8, а остатки от деления записываются от последнее частное в противоположном направлении. Например:
246/8 = 30 и остаток равен 6
30/8 = 3 и остаток равен 6
3 меньше 8, деление завершено.
Таким образом, 24610 = 3668.
Обратный перевод осуществляется путем разложения числа в развернутый вид:
3668 = 3*82 + 6*81 + 6*80 = 3*64 + 6*8 + 6*1 = 192 + 48 + 6 = 24610
Арифметические действия
Арифметические действия в восьмеричной системе счисления выполняются так же, как и в десятичной системе счисления. Большие числа удобнее всего складывать и вычитать столбиком. Только помните, что после 7 идет 10, то есть сумма восьмеричных чисел равна 3+5=10, а не восемь. Для сложения восьмеричных чисел при выполнении расчетов удобнее всего использовать таблицу.
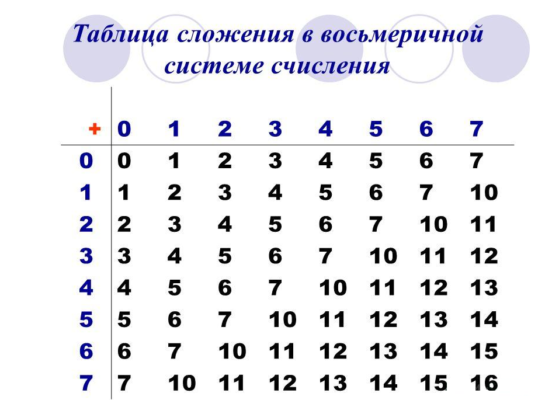
Например, сумма 34+25=61. Делалось это так. Сначала складываются младшие цифры 4+5=11 (см таблицу). Один остается в младшей цифре, а другой переносится в старшую цифру и прибавляется к сумме чисел 3+2=5. Итого — 61.
Что мы узнали?
Восьмеричная система счисления удобна для представления двоичных кодов и записи машинных инструкций при программировании. Основой этой системы является число 8. Триады используются для преобразования чисел из двоичных в восьмеричные и наоборот. Преобразование восьмеричных чисел в десятичную систему осуществляется путем поочередного деления частного и записи остатков деления. Обратный перевод осуществляется путем расширения числа до развернутого вида.








Комментирование закрыто