
Одним из частых видов неравномерного движения является движение тела с постоянным ускорением. Рассмотрим особенности такого движения, выведем его кинематическую формулу.
При этом, поскольку скорость – это векторная величина, то даже при постоянном модуле она может меняться, изменяя направление.
Изменение скорости может происходить с разной быстротой. Одна и та же скорость может быть достигнута с нулевой за различное время. Для оценки этой быстроты используется специальный параметр – ускорение.
Ускорение равно отношению изменения скорости движения ко времени этого изменения:
$$\overrightarrow a = {\overrightarrow v_2 – \overrightarrow v_1 \over t_2-t_1}={\overrightarrow{Δv} \over Δt}$$
Ускорение – это векторная величина, если движение с ускорением происходит не по прямой, а на плоскости или в пространстве, ее направление и модуль находятся по правилам действий с векторами.
Из формулы ускорения следует, что единицей ускорения является метр в секунду за секунду или метр в секунду в квадрате.

Скорость движения при постоянном ускорении
Движение с постоянным ускорением называется равноускоренным, независимо от того, увеличивает ли тело скорость или уменьшает. Хорошим примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха не играет роли. Еще Галилей установил, что все тела при падении увеличивают скорость одинаково, то есть движутся с равным ускорением.
Используя приведенную формулу, можно найти скорость падающего тела (и вообще любого тела, движущегося с постоянным ускорением) в любой момент времени. Если в принятой Системе Отсчета тело в момент времени $t_1=0$ двигалось со скоростью $\overrightarrow v_0$, и после этого двигалось с ускорением $\overrightarrow a$ его скорость в момент $t$ составит:
$$\overrightarrow v = \overrightarrow v_0 + \overrightarrow at$$
Это основная формула скорости при равноускоренном движении.
Графиком скорости при постоянном ускорении является прямая, пересекающая ординату в точке с координатой $v_0$, и направленная вверх, если ускорение положительно, или вниз, если ускорение отрицательно.
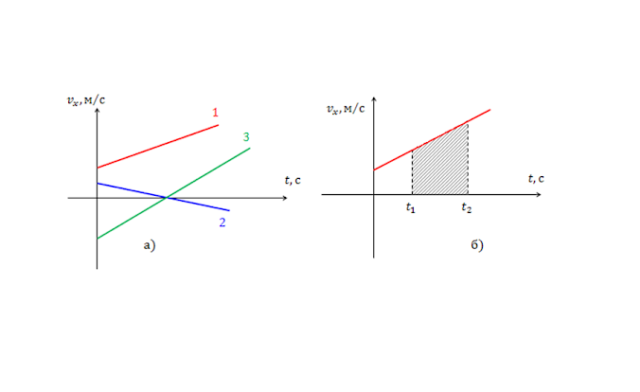
Перемещение при равноускоренном движении
Из графика скорости можно определить перемещение, учитывая, что величина перемещения равна площади фигуры под графиком.
В общем случае эта фигура представляет собой трапецию, высота которой равна $t$, а основания – $v_0$ и $v=at$. Используя формулу, уже известную в 10 классе из геометрии, получим:
$$x = {v_0+v\over 2}t$$
Учитывая векторный характер величин, а также то, что в начальный момент перемещение равно $x_0$, окончательно имеем:
$$\overrightarrow x =\overrightarrow x_0+\overrightarrow v_0t+{\overrightarrow at^2\over 2}$$
Это основная формула перемещения при равноускоренном движении. Отметим, что она представляет собой уравнение второй степени, то есть график перемещения при равноускоренном движении будет параболой.
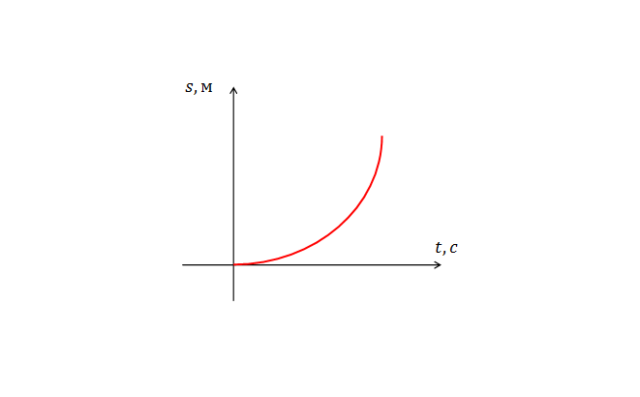
Обе приведенных формулы связывают скорость и перемещение материальной токи с моментом времени. Но, при решении задач иногда требуется, чтобы формула напрямую связывала скорость и перемещение. Выразив время из формулы скорости, и подставив его в формулу расстояния, получим:
$$x(t)=x_0+{v^2-v_0^2\over 2a}$$
Заметим, что данное соотношение имеет скалярный вид. Так происходит из-за присутствия действий умножения и деления, которые не применимы к векторным величинам, поэтому последнюю формулу можно использовать лишь только после проецирования векторов на оси координат.
Что мы узнали?
Ускорение – это величина, характеризующая быстроту изменения скорости движения. Если при движении ускорение не меняется, такое движение называется равноускоренным. График скорости при равноускоренном движении представляет собой наклонную прямую, график перемещения – параболу.








Комментирование закрыто