
Во многих случаях тело начинает движение из состояния покоя, то есть, из состояния с нулевой начальной скоростью. Поговорим кратко о движении тела без начальной скорости.
Например, пассажир движущегося поезда некоторое время сидит на своем месте, а потом переходит на другое место. В Системе Отсчета, связанной с рельсами, он постоянно движется. Однако, в Системе Отсчета, связанной с вагоном, он в нулевой момент времени покоится, и лишь спустя некоторое время начинает движение.

Таким образом, начальная скорость тела зависит от выбранной Системы Отсчета.
Формулы кинематики для случая нулевой начальной скорости
Если начальная скорость тела равна нулю, а тело через некоторое время переместилось, значит, на тело действовала некоторая сила, которая привела к появлению ускорения, в результате которого и произошло перемещение тела. Иначе говоря, тело двигалось с ускорением. То есть, можно использовать общие формулы кинематики для равноускоренного движения:
$$\overrightarrow x=\overrightarrow x_0+\overrightarrow v_0t+{\overrightarrow at^2\over 2}$$
$$\overrightarrow v=\overrightarrow v_0+\overrightarrow at$$
Подставив в эти формулы $\overrightarrow v_0 = 0$, получим:
$$\overrightarrow x=\overrightarrow x_0+{\overrightarrow at^2\over 2}$$
$$\overrightarrow v=\overrightarrow at$$
Если построить графики этих формул и сравнить их с общими графиками, то можно отметить следующие особенности.
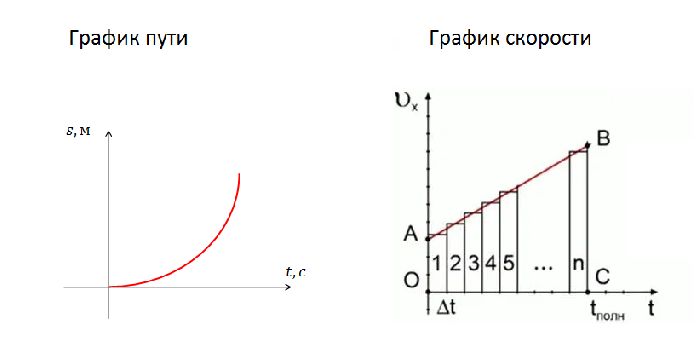
График пути представляет собой параболу, такую же, как при движении с начальной скоростью. Однако, эта парабола симметрична относительно оси ординат, и ее вершина пересекает эту ось. Следовательно, если тело двигалось с тем же ускорением до принятого в Системе Отсчета начального момента, то в этот момент перемещение тела имеет экстремальное (наибольшее или наименьшее) значение. Например, если рассматривается свободное падение тела, то нулевой момент будет соответствовать высшей точке траектории.
График скорости представляет собой прямую, имеющую тот же наклон, как и при движении с начальной скоростью, но, пересекающую начало координат.
Выбор Системы Отсчета
Формулы, описывающие движение тела без начальной скорости, проще. Поэтому при решении задач следует, по возможности, выбирать Систему Отсчета так, чтобы у рассматриваемого тела начальная скорость была равна нулю.
Особенно простая форма получается, если и начальное перемещение тела также будет нулевым. Например, для описанного выше примера перехода пассажира с одного места на другое – Систему Отсчета разумно связать с креслом пассажира.
Что мы узнали?
Формулы кинематики для движения без начальной скорости проще. Поэтому следует по возможности выбирать Систему Отсчета так, чтобы рассматриваемые тела в этой системе не имели начальной скорости.








Комментирование закрыто