
Из курса физики 10 класса известно, что газ — это состояние вещества, в котором беспорядочно движущиеся молекулы слабо связаны друг с другом. В отсутствие внешних сил они стремятся равномерно распределиться по всей предоставленной ёмкости. При этом молекулы сталкиваются друг с другом и со стенками, сила их соударений складывается в постоянное давление. Кратко рассмотрим эту тему, выведем формулу давления газа.

Такой моделью является идеальный газ.
Определение идеального газа включает следующие условия:
- он состоит из молекул, представляющих собой материальные точки;
- молекулы никак не взаимодействуют между собой;
- движение молекул хаотично и подчиняется законам ньютоновской механики;
- соударения между молекулами абсолютно упругие, то есть сумма кинетических энергий молекул при столкновении не меняется.
В реальных газах, строго говоря, ни одно из этих условий не выполняется. Однако с достаточной степенью точности примером идеального газа можно считать воздух и отдельные газы, входящие в его состав при нормальных условиях (давление порядка атмосферного и температура порядка 300 К).

Давление идеального газа
Для вывода формулы давления идеального газа представим идеальный газ, молекулы которого имеют массу $m_0$ и среднюю скорость $v_{ср}$. В результате соударения эта скорость меняет направление на противоположное. Таким образом, импульс, передаваемый такой молекулой при ударе, оказывается вдвое больше её импульса до удара и равен:
$$Δp =2m_0|v_{ср}|$$
Пусть количество молекул в единице объёма (концентрация) равно $n$. В этом случае число ударов на некоторой площади $S$ за время $t$ равно:
$$Z=n|v_{ср}|St$$
Все вместе эти удары передадут импульс силы:
$$Ft=2m_0|v_{ср}|Zt$$
Из двух последних формул можно получить:
$$F=2nm_0v_{ср}^2S$$
Молекулы газа движутся хаотично во всех шести направлениях (вверх-вниз, вправо-влево, вперёд-назад), а мы рассматривали только удары в одном направлении — о площадь $S$. Значит, среднее значение силы в шесть раз меньше:
$$\overline F={1\over 3}nm_0v_{ср}^2S$$
Давление равно отношению силы к площади её приложения:
$$p={\overline F \over S}$$
Подставив сюда предыдущую формулу, получим окончательно:
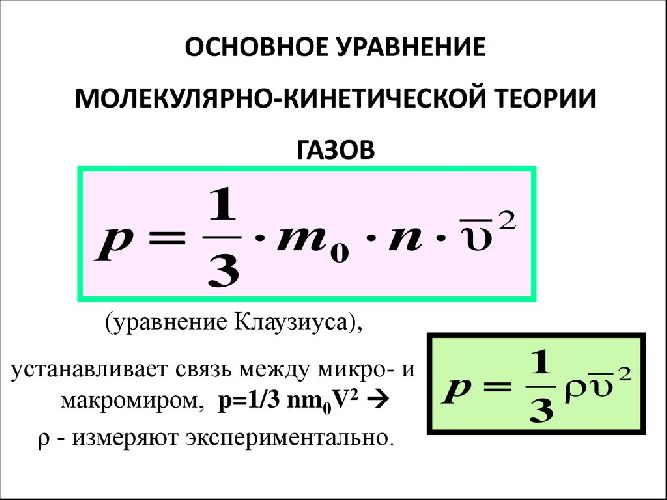
$$p={1\over 3}nm_0v_{ср}^2$$
Мы получили формулу давления идеального газа, которая также называется основным уравнением молекулярно-кинетической теории (МКТ).
Иногда удобно выразить давление газа через среднюю кинетическую энергию молекулы. Напомним, что средняя кинетическая энергия молекулы равна:
$$E_{ср}={m_0v_{ср}^2\over 2}$$
А значит, формула давления может быть преобразована к виду:
$$p={2\over 3}nE_{ср}$$
Отметим, что скорость и средняя кинетическая энергия молекулы прямо пропорциональны температуре. Поэтому в полученную формулу неявно входит и температура газа.
Что мы узнали?
Идеальный газ — это упрощённая модель вещества в газообразном состоянии. Реальные газы хорошо описываются этой моделью в нормальных условиях. Давление идеального газа создаётся в результате ударов отдельных молекул, оно пропорционально концентрации молекул газа и средней кинетической энергии молекулы.








Комментирование закрыто