
Для всех известных на сегодня видов энергии (механическая, внутренняя, электромагнитная, ядерная и др.) выполняется фундаментальный закон сохранения и превращения энергии. Рассмотрим действие этого закона на примере механической энергии, в состав которой входят потенциальная и кинетическая энергии. Выясним, с помощью каких формул вычисляются разные виды механической энергии.
Чем большей энергией обладает тело, тем большую работу оно способно совершить. То есть энергия это не что иное, как запас работы, которую может совершить тело, изменяя свое состояние.
Кинетическая энергия
Физическая величина, равная половине произведения массы тела m на квадрат его скорости v2, называется кинетической энергией тела Ek:
$ E_k = {m*v^2\over 2} $ (2).
Тогда для работы A получим следующую формулу:
$ A = E_{k1} — E_{k0} $ (3),
где:
Eк0 — начальная кинетическая энергия тела;
Eк1 — конечная кинетическая энергия после действия силы, изменившей скорость тела.
Из формулы (3) следует, что работа силы, приложенной к телу, равна изменению кинетической энергии тела. Таким образом, любое движущееся тело обладает кинетической энергией.

Потенциальная энергия
Потенциальная энергия — это энергия, которая зависит от взаимного расположения взаимодействующих тел (или частей одного тела). Одиночное тело, не взаимодействующее с другими телами, не может обладать потенциальной энергией. В состав механической энергии включают два вида потенциальной энергии: энергию тела, на которое воздействует сила земного притяжения и энергию упруго деформированного тела.
Сила тяжести и потенциальная энергия
По аналогии с кинетической энергией определим работу A, совершенную силой тяжести FТ по перемещению тела массой m с высоты h2 от поверхности Земли до высоты h1. При этом, если h2 > h1, то значит, тело переместилось сверху вниз. Считаем силу тяжести постоянной, независящей от высоты и равной m*g, где g = 9,8 м/с2 — ускорение свободного падения. Тогда, воспользовавшись формулой (1), получим:
$ A = m*g*(h_2 — h_1) $ (4)
Таким образом, работа силы тяжести по перемещению тела с высоты h2 на высоту h1 равна изменению величины m*g*h, которая называется потенциальной энергией тела Ep:
$ E_p = { m*g*h }$ (5).
Величина работы есть не что иное, как изменение потенциальной энергии тела, которую называют гравитационной, так как он обусловлена силой притяжения к Земле (от латинского gravitas — притяжение):
$ A = E_{p2} — E_{p1} $ (6).
где:
Ep1 — потенциальная энергия тела на высоте h1;
Ep2 — потенциальная энергия тела на высоте h2.
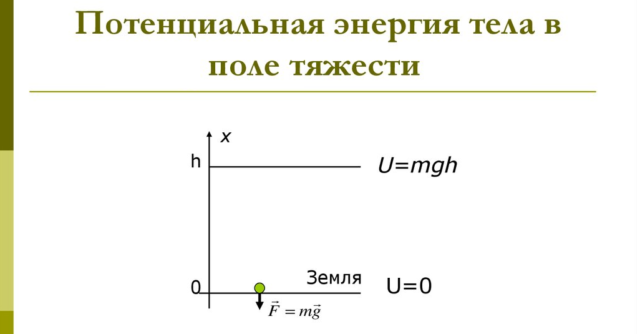
В отличие от кинетической энергии, которая может быть только положительной, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m, находящееся на глубине h от поверхности земли, обладает отрицательной потенциальной энергией. :
$ E_p = − { m*g*h }$
Потенциальная энергия упруго деформированного тела
Примером этого вида потенциальной энергии может служить пружина, которая после деформации (сжатии или растяжения) приведет в движение прицепленный к ней груз, то есть совершит работу. Пользуясь формулой (1) и законом Гука для силы упругости, можно получить выражение для потенциальной энергии упруго деформированной пружины:
$ Ep = {k*x^2\over 2} $ (7),
где: x — величина деформации (сжатие или удлинение пружины), k — коэффициент жесткости пружины.
Закон сохранения механической энергии
Полная механическая энергия тела EM равна сумме потенциальной и кинетической энергий:
$ {E_м = E_p + Е_k} $ (8).
К середине XIX века физики разных стран на основании многочисленных исследований физических и химических процессов сформулировали закон сохранения и превращения энергии. В общем виде закон звучит так:
При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.
Действие этого закона для механической энергии рассмотрим на классическом примере подброшенного вертикально вверх металлического шарика. При подъеме шарика его скорость убывает, так как на него действует сила земного тяготения. Согласно формулы (2) убывает и кинетическая энергия Ек. В то же время, с ростом высоты h растет потенциальная энергия Ep (см. формулу (5)). Воспользовавшись формулами (2), (4) и (5) можно получить, что в любой точке уменьшение величины Ек равно увеличению величины Ep. В момент прекращения движение вверх (в верхней точке подъема), вся кинетическая энергия полностью перейдет в потенциальную. При движении (падении) тела вниз происходит обратный процесс: потенциальная энергия тела Ep превращается в кинетическую Ек.
Приведенный пример иллюстрирует выполнение закона сохранения и превращения механической энергии, так как при подъеме уменьшение кинетической энергии полностью компенсируется ростом потенциальной (при падении — наоборот). Если потенциальная энергия у поверхности земли равна нулю, (т.к. h=0). то на любой высоте будет выполняться равенство:
$ {E_м = E_p + Е_k = {m*v_0^2\over 2}} $ (9),
где: v0 — начальная скорость шарика.
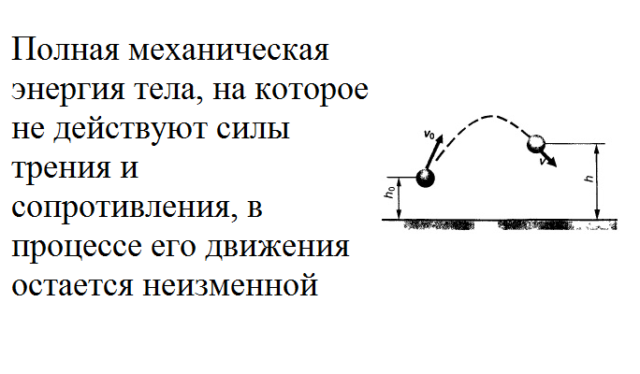
Для случая механической энергии закон сохранения можно сформулировать так: если между телами системы действуют исключительно силы упругости и силы тяготения, то сумма потенциальной и кинетической энергий остается постоянной, то есть механическая энергия сохраняется.
Если между телами кроме сил тяготения и упругости действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии будет превращаться во внутреннею энергию тел, то есть перейдет в тепло. Общий закон сохранения энергии, конечно, остается в силе. Происходит только перераспределение части механической энергии в тепловую (внутреннею).
Что мы узнали?
Итак, при изучении данной темы мы узнали что механическая энергия тела состоит из кинетической и потенциальной энергий. Энергия — это запас работы, которую может совершить тело, изменяя свое состояние. Закон сохранения энергии в механике утверждает, что энергия не возникает и не исчезает, а только превращается из одной формы (потенциальной энергии) в другую — кинетическую. Механическая энергия сохраняется в случае отсутствия силы трения.








Комментирование закрыто