Закон Ома для замкнутой цепи

Соотношение, которое связывает ток в цепи с ее сопротивлением и напряжением, называется законом Ома. Закон Ома имеет несколько форм. Кратко рассмотрим формулу закона Ома для замкнутой цепи постоянного тока.

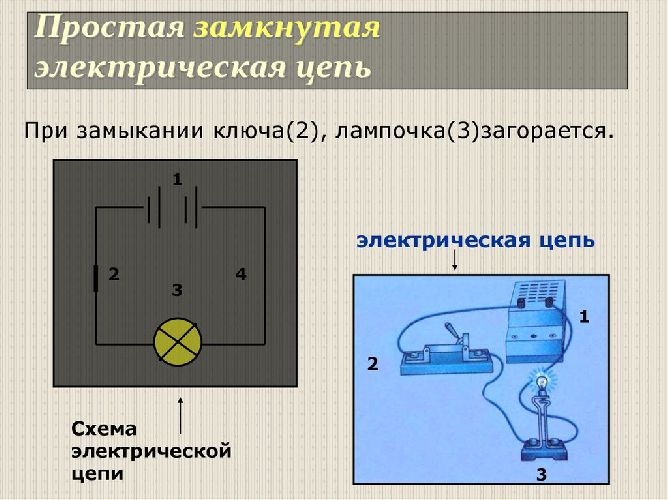
Элемент цепи, который является источником электрического поля, называется источником электродвижущей силы (ЭДС). Суть действия источника ЭДС в том, что внутри этого источника происходит постоянный перенос зарядов между клеммами с помощью сил, природа которых отличается от электрической (сторонних сил). При включении источника ЭДС в замкнутую цепь, сторонние силы создают на его клеммах разность потенциалов, и в замкнутой цепи начинает проходить ток.

Таким образом, главная характеристика источника ЭДС — это величина сторонних сил. Эта величина и обозначается термином «электродвижущая сила (ЭДС)». Она обозначается символом $mathscr{E}$ и равна отношению работы сторонних сил к перенесенному заряду:

$$mathscr{E}={A_{ст}\over q}$$

Из данной формулы видно, что размерность ЭДС та же, что и размерность напряжения, — джоуль на кулон, или вольт.

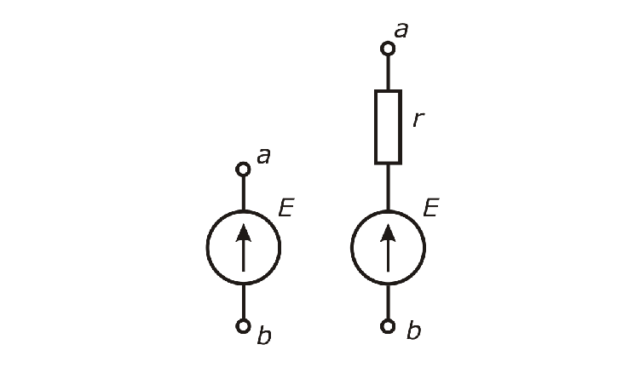
Вторая характеристика источника ЭДС — внутреннее сопротивление. Вещество источника тока, точно так же, как и любой другой проводник, обладает некоторым электрическим сопротивлением, на котором теряется часть энергии. Физический смысл этого сопротивления такой же, как и у сопротивления проводника или нагрузки, и размерность та же — омы.

Формула закона Ома для замкнутой цепи

Выведем формулу закона Ома для замкнутой цепи.

Сторонние силы, перемещая заряд $Δq$ за время $Δt$, совершают работу:

$$А_{ст}=mathscr{E}q$$

Ток, по определению, равен отношению заряда, прошедшего по проводнику ко времени прохождения, то есть:

$$I={Δq\over Δt}$$

Подставив значение заряда из этой формулы в предыдущую, получим:

$$А_{ст}=mathscr{E}IΔt$$

Вся эта работа будет выделена в виде тепла на сопротивлении цепи. Сопротивление цепи состоит из двух компонент: сопротивление самой цепи $R$ и сопротивление источника ЭДС $r$. С учетом закона Джоуля-Ленца:

$$ А_{ст}=I^2RΔt+I^2rΔt$$

Приравнивая левые части формул, получаем:

$$mathscr{E}IΔt=I^2RΔt+I^2rΔt$$

После сокращений и преобразований имеем:

$$I={mathscr{E}\over R+r}$$

Особенности использования формулы

В формулировку закона Ома для замкнутой цепи входит только одно сопротивление и одно значение ЭДС. Однако в реальных цепях много элементов, и возможны несколько источников ЭДС. В этом случае используется эквивалентное сопротивление цепи, которое находится по специальным формулам преобразования цепей. В качестве значения внутреннего сопротивления используется сумма сопротивлений источников. А в качестве значения ЭДС используется алгебраическая сумма ЭДС источников.

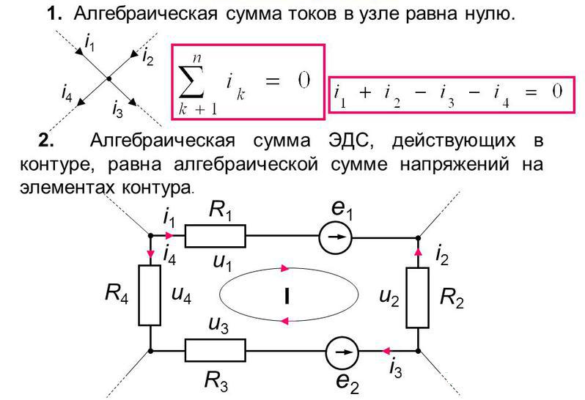
Если цепь очень сложна и составлена из многих узлов, связанных в сложное «кружево», для нахождения тока по такой цепи используются законы Кирхгофа и составление систем уравнений.