Закон Ома для участка цепи

Наравне с законами Кирхгофа, закон Ома для участка цепи – один из ключевых во всей электротехники. При проектировании электросетей любой сложности закон Ома становится необходимым инструментом, так как позволяет рассчитывать требуемые для нужного результата параметры сети.

$I = frac {U}{R}$, где I – сила тока, измеряемая в амперах, U – напряжение, измеряемое в вольтах и R – сопротивление, измеряемое в омах. Дадим словесную формулировку закона: сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.

Из фигурирующих в уравнении величин ключевой является сопротивление. Оно зависит от параметров проводника:

• Становится больше с увеличением длинны проводника
• Уменьшается с ростом проводимости проводника и его площади сечения.

Объяснить это очень просто: чем больше путь, проходимый электронами, тем больше вероятность столкновений с атомами в узлах решетки. Это мешает движению тока. С другой стороны, увеличение площади сечения дает больше вариантов пути электронам, уменьшается вероятность соударений. Проводимость же – исключительно свойства проводящего вещества. Например, медь оказывает меньшее сопротивление, чем железо, поскольку является более проводимым.

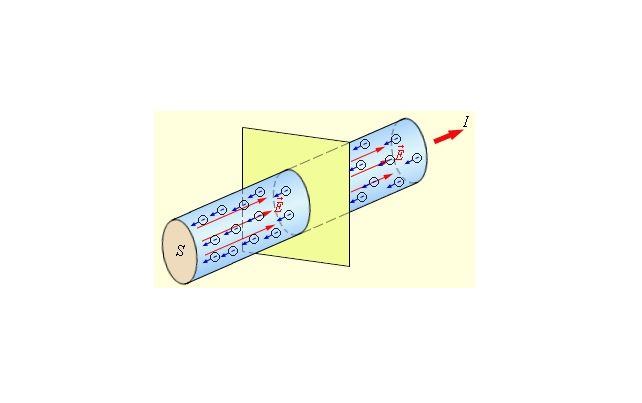
Закон Ома с точностью справедлив лишь для цепей, где действует идеальный источник тока. То есть такой, в котором нет внутреннего сопротивления. В противном случае применяется закон Ома для полной цепи.

Рассмотрим участок электрической цепи (рис. 2). В узлах 1 и 2 – потенциалы электрического поля $phi_1$ и $phi_2$. Между ними заключен элемент с сопротивлением R – резистор. К участку также подсоединен вольтметр.

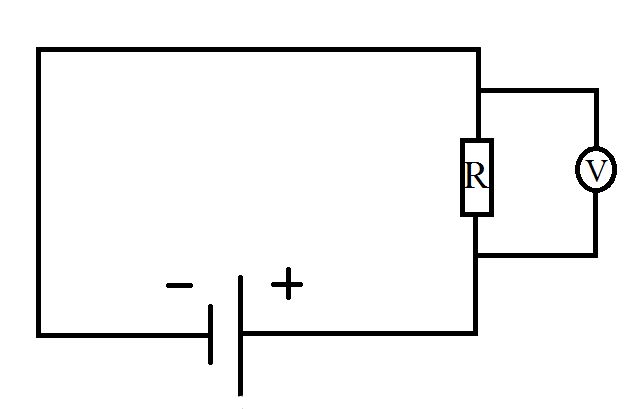
Тогда падением напряжения на данном участке электрической цепи будем называть величину, выраженную через закон Ома:

$U = I cdot R$

Падение напряжения – определение, сложившееся исторически. Речь идет об изменении значения потенциала электрического поля по мере продвижения вдоль проводника.

Для запоминания закона Ома используют правило, называемое треугольником Ома.

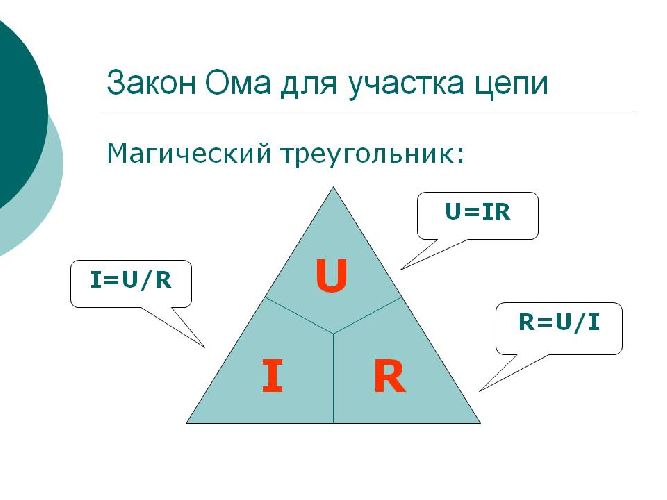
Техника работы с ним проста. Ту величину, которую нужно найти, закрываем пальцем, а две другие дают формулу для ее нахождения. Закрыв I, получим $frac {U}{R}$.

Задачи

Решение:

Запишем закон Ома для участка цепи:

$I = frac {U}{R}$

Подставив в него известные величины, получим:

$I = frac {10}{2} = 5 : А$

Теперь, зная, что сопротивление прямо пропорционально длине проводника, запишем:

$I = frac {U}{2R} = 2,5 А$

Решение:

Запишем закон Ома для участка цепи:

$I = frac {U}{R}$

Подставив в него известные величины и выразив R, получим:

$R = frac {U}{I} = frac {200}{0,1} = 2000 Ом : А$