
Закон Ома связывает в одной формуле электрические параметры, с помощью которых можно определить токи и напряжения на каждом элементе цепи. Данный закон можно распространить на всю электрическую цепь. Рассмотрим, как это происходит.
Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:
$$mathscr{E}={A_{ст}\over q}$$
Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:
$$1В={Дж\overКл}$$
Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.

Закон Ома для полной цепи
Когда в полной электрической цепи имеется источник ЭДС, в цепи возникает ток. Его величину можно найти, используя закон сохранения энергии и закон Джоуля-Ленца, выражающий энергию, выделяемую на электрическом элементе при прохождении по нему тока.
Если сторонние силы за время $Δt$ переместили заряд $Δq$, то, они совершили работу:
$$А_{ст}=mathscr{E}q$$
Заряд, переносимый сторонними силами внутри источника, пройдет по цепи за то же время $Δt$, а значит, сила тока в цепи будет равна:
$$I={Δq\over Δt}$$
Таким образом, величина работы сторонних сил:
$$А_{ст}=mathscr{E}IΔt$$
А согласно закону Джоуля-Ленца, ток $I$, прошедший через цепь, создаст некоторое количество теплоты. Во внешней цепи эта теплота выделится на сопротивлении внешней цепи $R$, а внутри источника тока – на его внутреннем сопротивлении $r$:
$$Q=I^2RΔt+I^2rΔt$$
Вся эта теплота, согласно Закону сохранения энергии, получена в результате работы сторонних сил ($А_{ст} = Q$), то есть:
$$mathscr{E}IΔt=I^2RΔt+I^2rΔt$$
Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:
$$I={mathscr{E}\over R+r}$$
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.
Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.
Сложные цепи с несколькими источниками тока
В замкнутой цепи может быть не один источник тока.
В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.
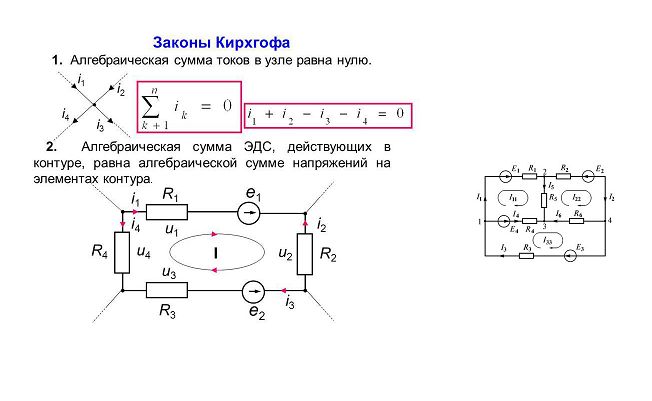
В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.
Что мы узнали?
Реальные источники тока обладают внутренним сопротивлением. Согласно Закону Ома для полной цепи, ток в замкнутой цепи равен отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника. Если в простой цепи несколько источников ЭДС, то общая ЭДС равна алгебраической сумме ЭДС источников. Для сложных цепей используются системы уравнений на основе правил Кирхгофа.








Комментирование закрыто