
С помощью понятия внутренней энергии в физике объясняются процессы, когда работа может совершаться покоящимся телом за счет энергии отдельных частиц, из которых состоит это тело. В большинстве случаев величина внутренней энергии тела представляет собой сумму потенциальной энергии взаимодействия молекул, составляющих тело, и кинетической энергии их хаотического теплового движения. Для описания тепловых явлений в веществах, находящихся в газообразном состоянии, используется модель идеального газа, которая позволяет получить достаточно простые формулы для величины внутренней энергии идеального газа.
- Молекулы имеют пренебрежимо малые размеры;
- Молекулы не взаимодействуют между собой (отсутствуют силы притяжения и отталкивания);
- Расстояния между молекулами много больше размеров молекул;
- Молекулы отталкиваются только при соударениях друг с другом и со стенками сосуда, где они находятся. Соударения описываются формулами из раздела механики для соударения шаров;
- Движение молекул происходит по законам Ньютона;
- Газ оказывает давление на стенки сосуда за счет ударов молекул газа.

Определение внутренней энергии
Внутренняя энергия вещества U — это сумма потенциальной энергии взаимодействия молекул Eп, составляющих тело, и кинетической энергии их хаотического теплового движения Ek:
$ U = { E_k + E_п } $ (1).
Для вычисления внутренней энергии газа Uг в формуле (1) можно пренебречь потенциальной составляющей энергии, то есть:
$ U_г = E_k $ (2).
Полная кинетическая энергия вещества Епк получается сложением энергий всех отдельных частиц:
$ Е^п_к = Е_1 + Е_2 + Е_3 +…. Е_N $ (2),
где N — общее число частиц в газе.
Частица массой m, движущаяся со скоростью v, обладает кинетической энергии Ек, которую можно вычислить с помощью формулы, полученной в разделе механики:
$ Ек = {m * v^2\over 2} $ (3).
Найти полную кинетическую энергию всех частиц газа помощью формул (2) и (3), не представляется возможным — для этого необходимо знать скорости и массы всех частиц, а также их общее количество. Учитывая, что только в одном моле вещества находится гигантское число молекул (6,023*1023!), становится понятно, что для нахождения внутренней энергии даже такой простой системы, как идеальный газ, требуется другая модель расчета с использованием таких макроскопических параметров, как давление p и температура T.
Кинетическая энергия и температура
Эксперименты показывали, что чем горячее вещество, тем с большими скоростями (“энергичнее”) двигаются частицы вещества. Изобретение термометра и введение величины температуры T, позволило ученым не только наблюдать за тепловыми явлениями, связанными с изменением температуры (нагревом и охлаждением), но и проводить измерения, накапливать результаты экспериментов в таблицах, анализируя полученные данные для разных веществ.
Во всех приборах, придуманных в ХVIII веке, измерение температуры сводилось к измерению длины столбика ртути, спирта или воды. Но оказалось, что самыми точными оказались газовые термометры. Дело в том, что жидкостные термометры работали только в ограниченном интервале температур. Наполняющие их вещества замерзали и кипели, и поэтому нельзя было измерять очень высокие и очень низкие температуры. Поэтому газовый термометр до сих пор используется как эталонный для всех температур, достижимых в лабораториях.
Ранее было получено уравнение состояния идеального газа — соотношение между давлением p, объемом V и абсолютной температурой (по шкале Кельвина) T, названное в честь его авторов уравнением Клапейрона-Менделеева:
$ p * V = {m\over μ} * R * T $ (4),
где:
μ — молярная масса газа, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
Газовая постоянная R равна:
$ R = k * N_a $ (5),
где: k =1,38*10-23 Дж/К — постоянная Больцмана, Na — число Авогадро.
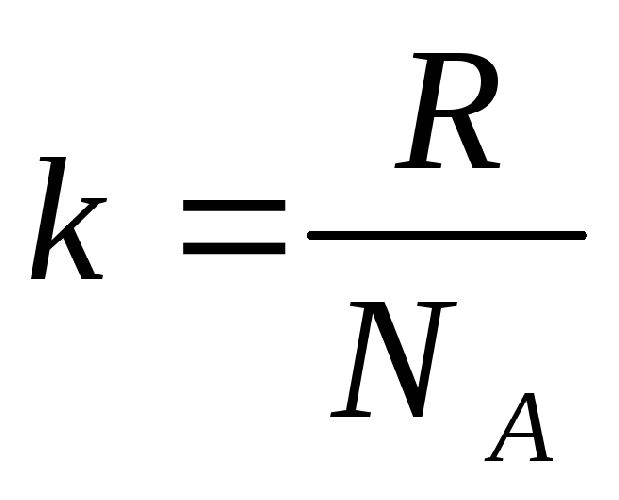
Тогда, из уравнений (4) и (5) получим выражение для давления идеального газа в виде:
$ p = n * k * T $ (6),
где: $ n = {m\over μ} * {Na\over V_об } $ — концентрация молекул, Vоб — объем.
В 1860 г. немецкий физик Рудольф Клаузиус получил для давления p одноатомного идеального газа следующую формулу, которую называют основным уравнением молекулярно-кинетической теории:
$ p = {1\over 3} * n * m * v^2_c $ (7),
где: v2c = <v2>ср — среднее арифметическое квадратов скоростей молекул.
Из двух формул (6) и (7) для величины давления p получаем:
$ p = {1\over 3} * n * m * v^2_c = n * k * T $ (7).
Разделив части уравнения (7) на n, и умножив обе части на 3/2, получим:
$ {m * v^2_с\over 2} = {3 \over 2} * k * T $ (8).
Левая часть уравнения (8) представляет собой величину средней кинетической энергии хаотического движения молекул (формула (3)). Таким образом:
$ Е_к = {3 \over 2} * k * T $ (9).
Последняя формула (9) демонстрирует, что средняя кинетической энергия хаотического движения молекул идеального газа, а значит и его внутренняя энергия, пропорциональна его температуре T.
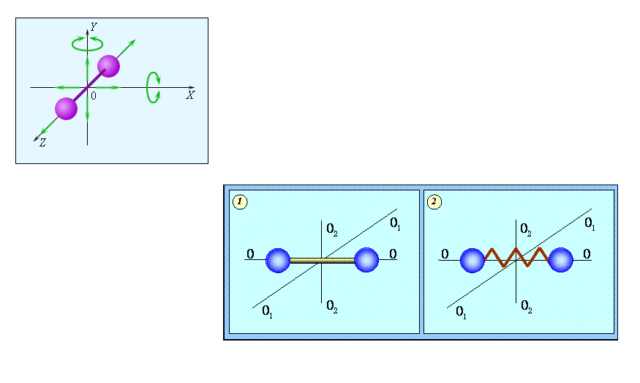
Представленные уравнения справедливы для случая одноатомного газа. Дело в том, что у молекул с большим числом атомов кроме чисто поступательного движения появляются дополнительные составляющие энергии: вращательная и колебательная. Поэтому к внутренней энергии добавится энергия вращения молекул и колебаний атомов внутри молекул. Например, молекула кислорода O2, имеет энергию $ {7\over 2} * k * T $, существенно превышающую энергию одноатомного газа (9).
Что мы узнали?
Итак, мы узнали какие условия должны выполняться для того, чтобы газ был идеальным. Внутренняя энергия идеального газа равна сумме кинетических энергий всех молекул газа. Средняя кинетическая энергия молекул одноатомного идеального газа прямо пропорциональна абсолютной температуре T. На основании уравнений Менделеева-Клапейрона (4) и Клаузиуса (7) получена формула зависимости средней кинетической энергии (9) от температуры T газа.








Комментирование закрыто