
Кинематика описывает движение, не рассматривая его причины. Для такого описания может использоваться несколько способов. Кратко рассмотрим векторный способ описания движения материальной точки.
Для определения времени и положения в пространстве используется система отсчета.
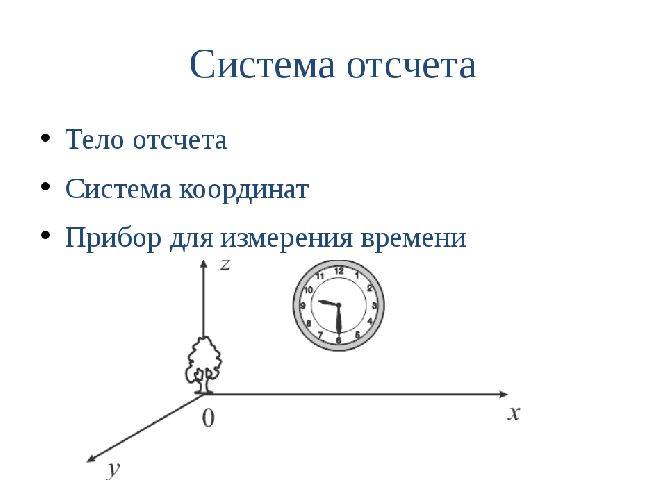
Моменты времени отмечаются с использованием некоторого эталонного процесса. В прошлом таким процессом было суточное вращение Земли, в настоящее время используется частота излучения возбужденных атомов цезия.
Положение в пространстве может задаваться несколькими способами, одним из которых является векторный.
Радиус-вектор
Как известно из геометрии, вектор — это отрезок на плоскости или в пространстве, для которого можно указать начало и конец. При этом для вектора важны не абсолютные координаты начала и конца в пространстве, а их разница. Положение вектора можно менять, сохраняя ее (параллельный перенос), сам вектор при этом не изменится.
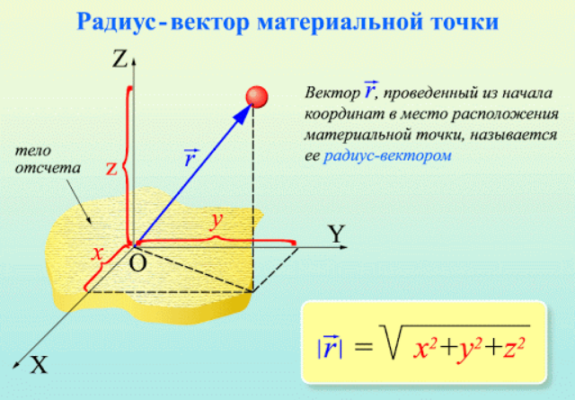
Последнее свойство векторов позволяет использовать их для однозначного задания положения точек в пространстве. Начало вектора помещается в начало координат, а конец вектора — в рассматриваемую точку. Вектор, построенный таким образом, называется радиус-вектором точки и обозначается $\overrightarrow r$.
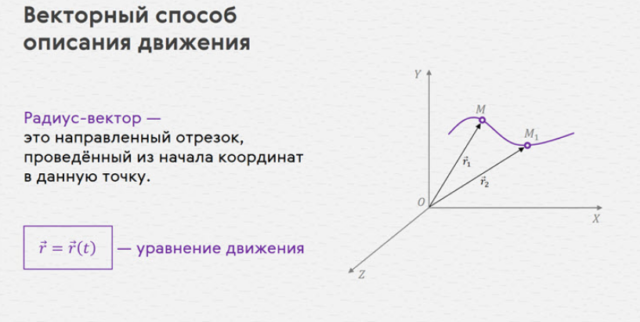
Векторная функция движения
При описании движения векторным способом задается соответствие между моментами времени и радиус-вектором:
$$\overrightarrow r=\overrightarrow r(t)$$
Данная формула — это уравнение движения точки, записанное в векторной форме. Функция $\overrightarrow r(t)$ — векторная функция, в которой используются правила действий с векторами.
Такая запись, как правило, заметно компактнее и проще, чем работа непосредственно с координатами точки. Однако математические действия с векторами требуют проецирования вектора на оси координат, алгебраического сложения длин, взятых с нужным знаком, и затем восстановления результата по проекциям. Поэтому векторный способ описания больше подходит тогда, когда требуется вывод законов и формул. В этом случае векторное уравнение позволяет выделить суть закона или формулы, не загромождая формулировки математическими выкладками.
Примером может служить векторная запись свободного падения тела с нулевой начальной скоростью и начальным положением $\overrightarrow {r_0}$:
$$\overrightarrow r=\overrightarrow {r_0}+{\overrightarrow { mathrm{g}} t^2\over 2}$$
Такая запись одинаково пригодна для любого числа осей координат и любого их направления. Если же записать то же уравнение в координатной форме, то потребуется несколько уравнений (по числу координатных осей), при этом для каждой оси ускорение свободного падения $mathrm{g}$ будет представлено соответствующей компонентой (проекцией). Можно задаться системой координат так, чтобы вектор $mathrm{g}$ был параллелен одной из осей. В этом случае формулы заметно упрощаются, однако возможность задаться удобной системой координат имеется не всегда.
Поэтому для физических законов векторная форма находит самое широкое применение. Она имеет компактную однострочную форму, при этом описывая движение сразу по всем координатным осям.
Что мы узнали?
В физике широкое применение находит векторный способ описания движения точки. Он имеет такую же точность, как координатный способ, но при этом учитывает сразу все координатные оси и записывается гораздо более компактно. Поэтому такой способ описания движения очень подходит для законов и формул: он позволяет выделить суть закона, не загромождая формулировку.








Комментирование закрыто