
Большинство движений в Природе являются неравномерными, они происходят с ускорением или замедлением. Рассмотрим понятие «ускорение материальной точки» более подробно.

Типичным примером неравномерного движения является свободное падение тел. За первые 0.1с падения тело проходит только 5см пути, и мгновенная скорость в конце этого промежутка составит 0,98 м/с. А в конце первой секунды тело пройдет 5м пути, и мгновенная скорость в этот момент будет равна 9,8 м/с. Как получить значение имеющейся мгновенной скорости в любой момент времени ?
Ускорение
Для исследования свободного падения можно измерять мгновенную скорость через равный промежуток времени (например, через 0.1с), и результаты представить в виде таблицы. В первом столбце будет момент времени, во втором – мгновенная скорость. В третьем столбце вычислим разницу мгновенной скорости между текущим и предыдущим моментом времени.
Получим :
|
t(сек) |
v(м/с) |
Δv(м/с) |
|
0.0 |
0.00 |
– |
|
0.1 |
0.98 |
0.98 |
|
0.2 |
1.96 |
0.98 |
|
0.3 |
2.94 |
0.98 |
|
0.4 |
3.92 |
0.98 |
|
0.5 |
4.91 |
0.98 |
Сразу бросается в глаза, что цифры в последнем столбце таблицы одинаковы. Это означает, что, хотя скорость постоянно меняется, разница скорости за одинаковый промежуток времени составляет одинаковую величину. Следовательно, для вычисления скорости в любой момент времени можно ввести специальную меру – ускорение.
Ускорение материальной точки равно отношению изменения скорости материальной точки к промежутку времени, за который это изменение произошло.
$$\overrightarrow a= {\overrightarrow v – \overrightarrow v_0\over t}$$
Из представленной формулы можно получить единицу измерения ускорения. Поскольку в системе СИ скорость измеряется в метрах в секунду, а время в секундах, то при делении получим метр в секунду за секунду (или метр в секунду в квадрате). Записывается, как $м/с^2$.

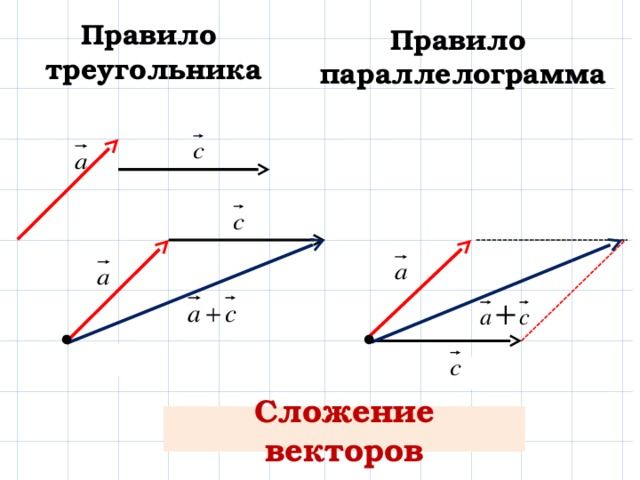
Также из этой формулы видно, что ускорение – это векторная величина, и направление ускорения материальной точки совпадает с направлением изменения скорости. При этом и величину, и направление этого изменения необходимо получать с помощью правил сложения векторов. В частности, если конечная скорость больше начальной, и направлена в том же направлении, то и ускорение будет направлено туда же. Если конечная скорость меньше начальной, то ускорение будет направлено в противоположную сторону. В случае, если вектора начальной и конечной скоростей не параллельны, для определения результата следует либо пользоваться правилом параллелограмма, либо проецировать вектора на оси координат, и складывать или вычитать проекции в зависимости от их направления, а потом по проекциям получать результат.
Что мы узнали?
При неравномерном движении скорость тела изменяется. Для характеристики быстроты этого изменения вводится специальная величина – ускорение. Ускорение равно отношению изменения скорости за некоторый промежуток времени к величине этого промежутка.








Комментирование закрыто