Уравнение вынужденных колебаний

Колебательные процессы широко распространены в Природе и в деятельности человека. Среди них немалая часть является вынужденными. Рассмотрим их особенности, выведем математическое уравнение таких колебаний.

Например, для случая пружинного маятника, внешнее воздействие должно сперва двигать маятник в одном направлении из точки равновесия, но, как только маятник из него выходит, направление воздействия должно сменяться, и действовать в противоположном направлении. Когда маятник оказывается отклонен в другом направлении, внешнее воздействие снова должно двигать маятник в первоначальную сторону.

Другой пример – процессы в электрическом колебательном контуре. Здесь также подведение энергии должно изменяться, в зависимости от направления тока в контуре в данный момент.

Уравнение вынужденных колебаний

Для описания вынужденных механических колебаний рассмотрим пружинный маятник с жесткостью пружины $k$, способный колебаться в вязкой среде. Сила сопротивления среды пропорциональна скорости движения (коэффициент пропорциональности $r$) и направлена в противоположном направлении.

Подведем к маятнику внешнее пульсирующее усилие. То есть, внешняя сила должна изменяться по гармоническому закону:

$$F=F_0cosomega t$$

Под действием этой внешней силы маятник выйдет из положения равновесия, и приобретет некоторую скорость. Следовательно, на него начнут действовать еще две силы:

• cила упругости пружины $F_{упр}=-kx$;
• cила сопротивления среды $F_{сопр}=-rv$.

Ускорение, получаемое маятником, согласно Второму Закону Ньютона, прямо пропорционально равнодействующей всех трех сил, и обратно пропорционально массе маятника:

$$a={F+F_{упр}+F_{сопр}\over m}={F_0cosomega t-kx-rv\over m}$$

Учтем, что скорость – это производная перемещения, а ускорение – производная скорости (и вторая производная перемещения). После преобразований получим:

$$x”+{r\over m}x’+{k\over m}x=F_0cosomega t$$

Мы получили дифференциальное уравнение вынужденных колебаний, описывающее рассмотренную систему. Данное является неоднородным дифференциальным уравнением второго порядка, оно решается в курсе высшей математики. Оно имеет вид:

$$x(t) = x_{св}(t)+x_{вын}(t)$$

где:

• $x_{св}(t)=А_0e^{-beta t}cos(sqrt {omega^2-beta^2}t+varphi_0)$ – уравнение затухающих колебаний;
• $А_0$ – начальная амплитуда колебаний;
• $varphi_0$ – начальная фаза колебаний;
• $beta = {r\over {2m}}$ – коэффициент затухания;
• $omega = sqrt {k \over m}$ – собственная частота колебаний маятника;
• $x_{вын}(t)=Аcos(omega_{вын}t+varphi_{вын})$ – уравнение вынужденных колебаний.

Резонанс

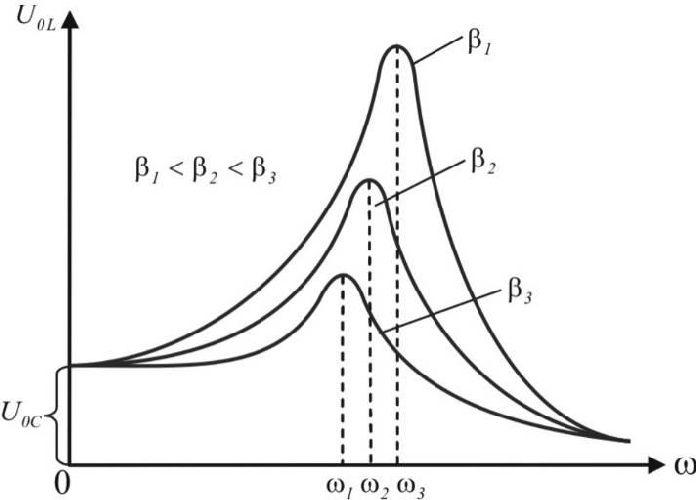
Компонента $x_{св}(t)$ в реальных системах за время $1\over beta$ уменьшится практически до нуля. А значит, уравнение вынужденных колебаний будет представлять из себя гармонические колебания с вынуждающей частотой, и некоторой амплитудой $A$, пропорциональной вынуждающей силе и зависящей также от близости вынуждающей частоты к собственной частоте колебаний маятника. Чем дальше вынуждающая частота к собственной частоте маятника, тем меньше будет значение $A$. При равенстве этих частот амплитуда резко возрастает, пока подводимая энергия не сравняется с потерями (они обычно растут при возрастании амплитуды).

Данное явление называется резонансом.