
Одним из достаточно частых движений, изучаемых физикой, является равноускоренное движение. Примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало. Поговорим на эту тему, рассмотрим уравнения равноускоренного движения для координаты и скорости.
$$\overrightarrow a = {\overrightarrow v – \overrightarrow {v_0} \over t }$$

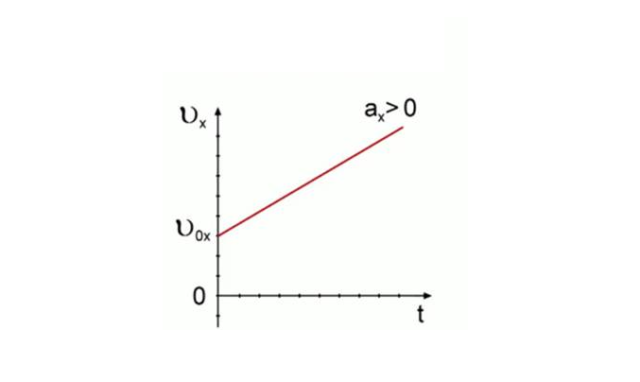
Уравнение скорости равноускоренного движения
Движение, при котором ускорение остаётся постоянным, называется равноускоренным. При этом нет разницы, увеличивается скорость или уменьшается. Из определения ускорения можно получить уравнение скорости при равноускоренном движении:
$$\overrightarrow v = \overrightarrow {v_0} + \overrightarrow a t $$
Можно видеть, что скорость при равноускоренном движении линейно зависит от времени. Следовательно, график скорости представляет собой прямую, пересекающую ось ординат в точке $v_0$, имеющую наклон вверх для положительного ускорения и вниз для отрицательного. Величина наклона тем больше, чем больше модуль ускорения.
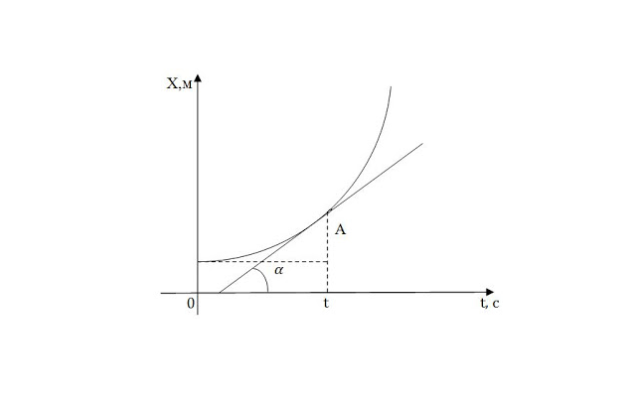
Уравнение координаты равноускоренного движения
Уравнение координаты при равноускоренном движении можно получить из графика скорости, учитывая, что координата движения равна площади, ограниченной графиком скорости.
Фигура, ограниченная графиком скорости, представляет собой трапецию, высота которой равна $t$, одно основание равно $v_0$, второе основание равно $v$. Из геометрии известно, что площадь трапеции равна полусумме оснований, умноженной на высоту. Величину $v$ при этом можно выразить из вышеприведённой формулы. То есть:
$$x={v+v_0\over 2}t={2v_0+at\over 2}t$$
Переходя к векторной форме и учитывая, что в начальный момент времени координата была равна $\overrightarrow {x_0}$, окончательно получаем:
$$\overrightarrow x=\overrightarrow {x_0}+\overrightarrow {v_0} t+ {\overrightarrow at^2\over 2}$$
Координата при равноускоренном движении имеет квадратичную зависимость от времени, график координаты является параболой.
Что мы узнали?
Равноускоренное движение — это движение, при котором ускорение остаётся постоянным. Уравнение скорости при равноускоренном движении представляет собой прямую зависимость от времени, его график является наклонной прямой. Уравнение координаты равноускоренного движения имеет квадратичную зависимость от времени, его графиком является парабола.








Комментирование закрыто