
Простейшим движением, которые изучается в рамках кинематики в 10 классе, является равномерное прямолинейное движение, то есть движение, траектория которого является прямой, а мгновенная скорость в любой из рассматриваемых моментов времени постоянна. Рассмотрим особенности такого движения, выведем уравнение равномерного прямолинейного движения.

Уравнение равномерного прямолинейного движения
Для вывода уравнения прямолинейного движения точки целесообразно выбрать ось координат, которая параллельна траектории движения. Пусть в нулевой момент времени материальная точка имеет координату $x_0$ и движется равномерно в положительном направлении.
Напомним, что скорость по определению — это отношение изменения координаты $Delta x$ к промежутку времени $Delta t$, за который это изменение произошло:
$$v={Delta x \over Delta t }$$
Если спустя время $t$ координата приняла значение $x$, следовательно, скорость точки равна:
$$v={x-x_0 \over t }$$
Движение равномерное, следовательно, какие бы мы моменты времени не брали, скорость в этой формуле будет постоянной, изменяться будет только координата с изменением времени.
Преобразовав формулу, получаем:
$$x= x_0 + vt$$
Полученная формула является уравнением равномерного прямолинейного движения.
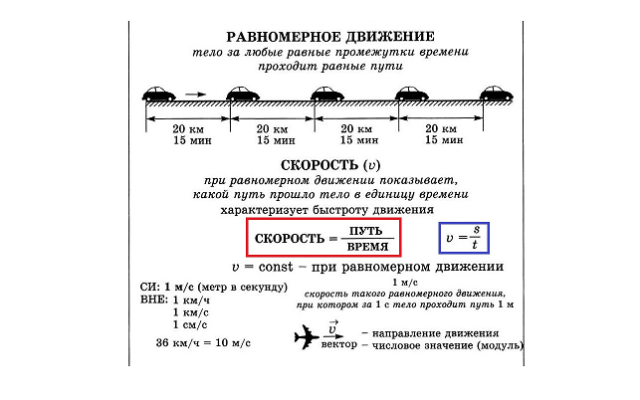
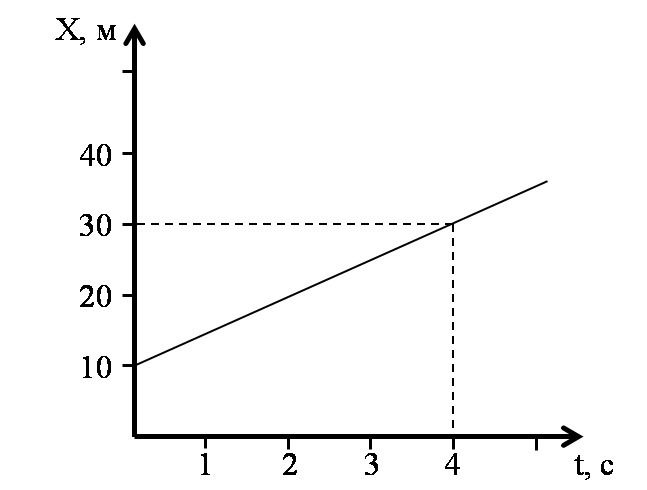
График равномерного прямолинейного движения
Из формулы координаты равномерного прямолинейного движения можно видеть, что это линейная зависимость. Графиком координаты при прямолинейном равномерном движении является прямая, расположенная под некоторым наклоном. Эта прямая пересекает ось ординат в точке $x_0$.
Наклон графика координаты равномерного прямолинейного движения зависит от скорости. Чем она выше, тем круче будет подниматься график. Если скорость отрицательна — график направлен вниз, и опускается тем сильнее, чем больше модуль скорости.
Отметим, что полученное уравнение даёт непосредственно координату $x$ точки в момент времени $t$, а не пройденный путь. Пройденный путь $S$ равен модулю разности начальной и конечной координат и может быть найден по формуле:
$$S=|x-x_0|$$
Что мы узнали?
Равномерное прямолинейное движение — это движение, траектория которого представляет собой прямую, а мгновенная скорость в любой точке траектории постоянна. Уравнение координаты равномерного прямолинейного движения представляет собой линейную зависимость, графиком которой является прямая, направленная под углом, зависящим от значения скорости.








Комментирование закрыто