
Для решения прикладных задач о плавлении тел важно было установить, сколько энергии требует этот процесс. В ходе экспериментов удалось выявить простую эмпирическую зависимость между количество теплоты, массой тела и некой константой, характеризующей вещество с точки зрения процесса плавления, которую назвали удельной теплотой плавления.

Что такое удельная теплота плавления
Наблюдение за плавлением различных кристаллических тел одинаковой массы позволило сделать вывод, что каждое из них требует различного количества теплоты. При этом те же вещества, но большей массы, требовали большего количества теплоты. Математически эту зависимость выражают так:
$Q=Cm$ (1), где С – некая константа пропорциональности. Ей дали название – удельная теплота плавления (или энтальпия плавления), и ввели для нее специальное обозначение – λ. Она характеризует, сколько теплоты нужно подвести к одному килограмму вещества, нагретому до температуры плавления, чтобы расплавить его в условиях постоянного давления.
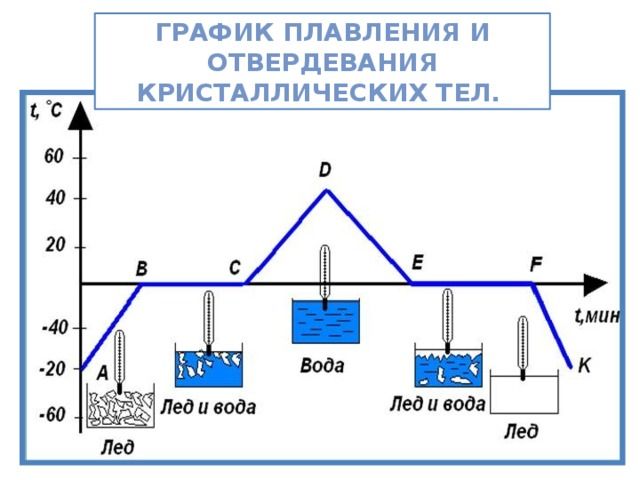
Величина удельной теплоты плавления зависит от свойств вещества. Так, например, для льда она равна 340 кДж/кг, а для золота – 66,6 кДж/кг. Из этого следует, что для плавления льда необходимо больше теплоты, чем для плавления золота.
Расчетная формула удельной теплоты плавления выводится из уравнения (1):
$ lambda= frac{Q_{плавления}}{m_{вещества}}$ – (2)
Из формулы не трудно понять, в чем измеряется энтальпия плавления. Если теплота – в джоулях, масса – в килограммах, то результат их деления – в Дж/кг.
Задачи
- Какое количество теплоты необходимо подвести к котлу, чтобы расплавить V метров кубических снега плотностью ρ? Удельную теплоту плавления снега принять за λ, удельную теплоемкость за с.
Решение первой задачи
Обозначим за $t_1$ начальную температуру льда, за $t_2$ – температуру плавления.
Тогда на нагрев льда до температуры плавления будет затрачено $Q_1 = cm(t_2-t_1)$ Дж или, выражая массу через объем и плотность, $Q_1 = c rho V(t_2-t_1)$ Дж.
На плавление льда будет затрачено $Q2 = rho V lambda$ Дж.
Тогда общее количество теплоты $Q = Q_1 + Q_2 = rho V(c(t_2-t_1) + lambda)$
- 1 литр кипятка вылили на кусок льда массой 2 кг, взятого при температуре 0̊ С. Какая часть льда расплавится?
Решение второй задачи
Из литра кипятка при его остывании выделяется $Q = cm(t_1-t_2) = cmt_1$ Дж, так как $t_2=0$.
Масса льда, которая расплавится данным количеством теплоты, $m_2 = frac{Q}{λ} = frac {cmt_1}{λ} = frac {{4200}times{100}}{340000} = 1,24$ кг.
Тогда исходную массу разделим на массу расплавленного льда:
$frac {m_1}{m_2} = frac {1,24}{2} = 0,62$ или 62% – часть льда, которая расплавится.
Что мы узнали?
В ходе урока мы узнали, что называется удельной теплотой плавления (константа пропорциональности между количеством теплоты и массой вещества в процессе плавления), какой буквой греческого алфавита она обозначается, узнали, как найти ее.








Комментирование закрыто