
Из курса физики 11 класса известно, что в электрическом контуре могут существовать свободные электромагнитные колебания. Рассмотрим основные особенности этого явления.
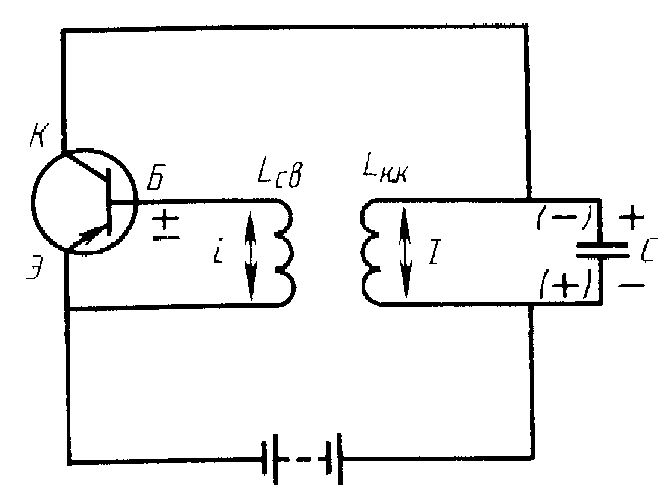
Полностью заряженный конденсатор имеет на обкладках некоторое напряжение. Поскольку сопротивление катушки очень мало, получается, что конденсатор закорочен через это сопротивление и должен быстро разряжаться.
Однако как только через катушку начинает проходить ток разряда, в результате явления самоиндукции в катушке возникает ЭДС, направленная так, чтобы противодействовать этому току. В итоге ток разряда не может сразу иметь большую величину. Потребуется некоторое время для его нарастания.
По мере того, как нарастающий ток проходит по катушке, конденсатор разряжается, и напряжение на нем падает. При уменьшении напряжения до нуля ток через катушку должен также уменьшиться до нуля, но ЭДС самоиндукции по-прежнему противодействует этому уменьшению. Поэтому, несмотря на то, что напряжение на конденсаторе упало до нуля, ток через катушку не может сразу уменьшиться и некоторое время продолжает проходить через катушку, одновременно заряжая конденсатор (сейчас в другом направлении). В момент, когда ток полностью упадет до нулевого значения, конденсатор опять окажется заряжен. На нем вновь будет напряжение, которое начнет разряжаться через катушку индуктивности.
Таким образом, напряжение на конденсаторе будет испытывать постоянные колебания.
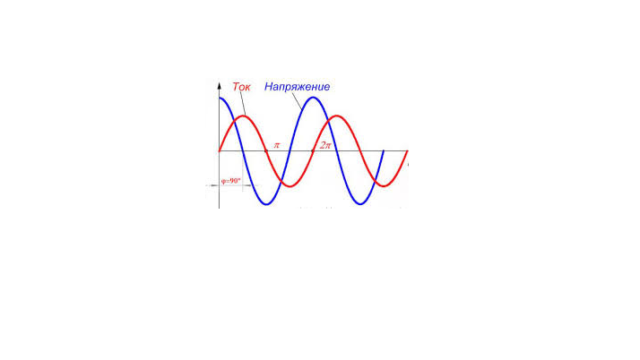
Обратите внимание, что максимальные значения напряжения и тока не совпадают во времени, они всегда сдвинуты по фазе.
Формула Томсона
Частота колебаний, возникающих в контуре, как можно понять из описания, зависит от емкости конденсатора и индуктивности катушки. Для нахождения этой частоты учтем, что энергия свободных электромагнитных колебаний в контуре существует в двух формах:
- в форме заряда конденсатора: $W_C={q^2\over 2C}$;
- в форме магнитного поля катушки: $W_L={Li^2\over 2}$.
Сумма этих величин будет постоянна: $W_C+W_C=const$. Кроме того, постоянной является скорость изменения этих видов энергии. А поэтому можно получить эти скорости (для этого берутся производные из обоих формул) и приравнять их друг другу, получив уравнение. После преобразований можно получить формулу, впервые выведенную У. Томсоном:
$$omega ={1\over sqrt {LC}}$$
Или для периода колебаний:
$$T ={2pi\overomega}=2pi sqrt {LC}$$
Данная формула предполагает отсутствие в контуре потерь. В реальном контуре элементы неидеальны, потери возникают, поэтому свободные колебания в реальном контуре всегда затухающие. Чтобы колебания в реальном контуре были постоянными, вводятся специальные элементы, обеспечивающие обратную связь и компенсирующие потери энергии в контуре.
Что мы узнали?
Свободные электромагнитные колебания — это колебания напряжения и тока, происходящие под действием внутренних сил системы. Простейшей такой системой является колебательный контур, состоящий из конденсатора и катушки индуктивности. Частота свободных колебаний в контуре определяется формулой Томсона.








Комментирование закрыто