
Температура — это уровень внутренней энергии, заключённой в хаотическом движении молекул вещества. Скорость конкретной молекулы может иметь весьма широкий диапазон, однако скорость большинства молекул лежит в достаточно узких пределах, поэтому в молекулярной физике используется среднее значение этой скорости. Как же оно определяется?
Когда число объектов очень велико (например, число молекул в теле), этот метод является единственно возможным. Более того, значение, полученное для одного конкретного объекта, практически не играет роли.
В таких случаях используется специальное значение, при котором суммарная ошибка параметра для всех объектов будет наименьшей. Это значение называется средним значением физической величины. Среднее значение может рассчитываться несколькими способами.

Скорость молекул газа
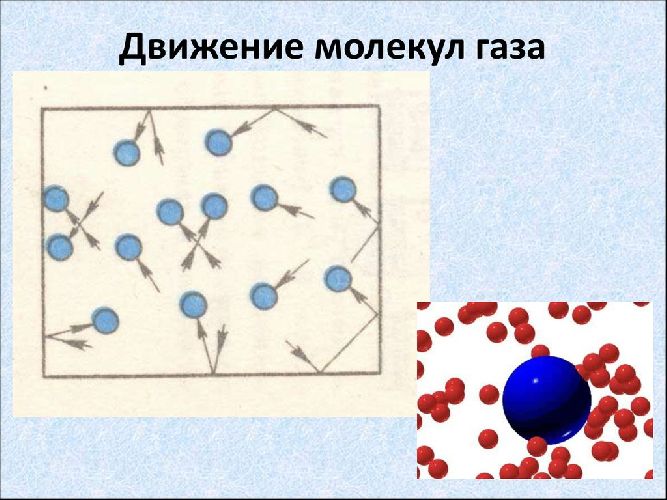
Газ — это хороший пример системы, которая состоит из большого числа движущихся объектов (молекул), при этом скорость каждой отдельной молекулы не имеет значения, и единственный способ оценки молекулярных движений — использование средней скорости.
Простейший способ нахождения среднего значения — это суммирование всех значений и деление суммы на количество значений. Такое среднее называется средним арифметическим.
Для скорости молекул такое среднее не подходит. Скорости молекул имеют самые разные направления, и, какое бы направление мы не взяли, всегда окажется, что по этому направлению и против него движется одинаковое число молекул. Простая сумма скоростей будет равна нулю. Поэтому здесь используется среднее значение квадрата скорости молекул.
$$\overline{v^2} = {v^2_1+v^2_1+…+v^2_N \over N}$$
Особенности среднеквадратичного значения
Квадрат любого ненулевого числа положителен, поэтому значение в приведённой формуле также всегда будет положительным.
Ещё одно преимущество использования средней квадратичной скорости молекул состоит в том, что кинетическая энергия материальной точки находится по формуле:
$$E={mv^2 \over 2}$$
Получается, что средняя квадратичная скорость молекул газа удобна для нахождения средней энергии молекулы, а она, в свою очередь, связана с макроскопическими параметрами — с температурой и давлением. Поэтому именно среднеквадратичная скорость используется в большинстве формул молекулярно-кинетической теории.

Что мы узнали?
Средняя квадратичная скорость молекул газа — удобный показатель, широко использующийся в молекулярно-кинетической теории для определения макроскопических параметров — температуры и давления.








Комментирование закрыто