
Большое количество задач классической механики требуют учета силы трения скольжения, ее учитывают и при проектировании различных механизмов, чтобы подобрать смазочные материалы или сделать конструкцию, при которой трение минимизируется. Поэтому необходимо понимать ее причины и уметь рассчитывать.
Трение обусловлено тем, что на микроуровне всякая поверхность шероховата. Неровности цепляются друг за друга и препятствуют движению.

Если внешняя сила достигает предельного значения, равного наибольшей силе трения покоя, груз начинает двигаться. Тогда возникает трение скольжения. Существует набор законов, названных в честь Кулона, открывшего их, которые описывают это явление.
Сила трения скольжения:
- Направлена вдоль поверхности соприкосновения и препятствует причинам движения.
- Не зависит от площади соприкосновения.
- Пропорциональна нормальной реакции опоры.
- Пропорциональна безразмерному коэффициенту трения.
Расчет силы трения скольжения
Для расчета силы трения скольжения допускают, что она не зависит от скорости и приблизительно равна наибольшему значению трения покоя. При невысоких скоростях такое приближение позволяет производить расчеты с достаточной точностью. Тогда формула силы трения скольжения запишется так:
$F_{тр} = mu N$, которая называется формулой Кулона-Амонтона и является математическим выражением третьего закона Кулона. При движении по горизонтальной поверхности $N = mg$
$mu$ – коэффициент трения скольжения, значение которого примерно равно коэффициенту трения покоя.
В том случае, если тело движется по наклонной поверхности, $F_{тр} = mu mgsin varphi$, где $varphi$ – угол наклона поверхности.
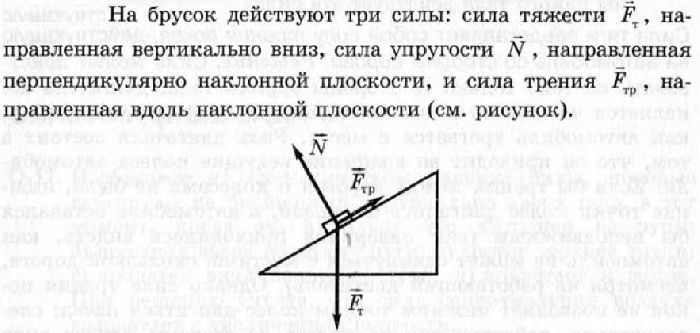
Когда поверхности сухие, трение называют сухим. Выделяют и другие виды: с сухой смазкой, жидкостное (влажная смазка), смешанное, когда чередуются влажные и сухие участки поверхностей.
Задачи
- Тело тянут на вершину горы с силой, равной 28 Н. Масса тела – 2 кг, угол наклона горы – 30˚, ускорение – 1 м/c2. Найти коэффициент трения скольжения.
Решение первой задачи
Запишем второй закон Ньютона в векторной форме:
$$m vec a = vec F_{тр} + m vec g + vec N + vec F$$
И в проекциях на оси:
Ох: $ma =F – F_{тр} – mgcos varphi$ – (1)
Оу: $N=mgsin varphi$ – (2)
Подставляя (2) в (1), получим:
$ma =F – mu mgsin varphi – mgcos varphi$, тогда коэффициент трения скольжения будет равен:
$$mu ={F \over mgsin varphi} – {a \over gsin varphi} – ctg varphi = 0,87$$.
- Велосипедист едет по кольцу радиуса 10 м со скоростью 10 м/с. Каков предельный угол, на который может наклонятся велосипедист?
Решение второй задачи
Запишем второй закон Ньютона в векторной форме:
$$m vec a = vec F_{тр} + m vec g + vec N$$
И в проекциях на оси:
Ох: $ma = F_{тр}$
Оу: $N=mg$
Из прямоугольного треугольника, составленного на вектора силы трения и нормальной реакции опоры, найдем:
$$ctg varphi = {F_{тр} \over N}$$
Тогда $ma = F_{тр} = Nctg varphi = mgctg varphi$. Выразим отсюда $ctg varphi$:
$ctg varphi = {a \over g}$, но $a = {v^2 \over R}$, поэтому $ctg varphi = {v^2 \over Rg} = {100 \over 10g} = 1$. Отсюда следует, что предельный угол равен 45˚.
Что мы узнали?
В ходе урока было установлено, от чего зависит сила трения скольжения и какова ее природы, были рассмотрены законы, характеризующие ее, и расчетные формулы, введены понятие коэффициента трения скольжения и виды трения скольжения. В завершении урока решены несколько задач.








Комментирование закрыто