Принцип суперпозиции полей

Одним из важнейших принципов, существующих в электростатике, является принцип суперпозиции полей. Кратко рассмотрим суть этого принципа, выведем его математическую формулу.

Даже силы трения можно представить в виде поля сил трения, поскольку трение также оказывает на движущиеся соприкасающиеся тела силовое действие.

Сложение действия полей

Что произойдет с зарядом, на который действует несколько полей ?

Опыт показывает, что сила, действующая на заряд со стороны поля, не зависит от других сил, тоже действующих на заряд. При этом их источником могут являться другие поля. Фактически, несколько полей будут действовать на заряд независимо, каждое будет создавать силу, точно такую же, как если бы это поле в точке было бы единственным.

Таким образом, если заряд помещен одновременно в несколько электрических полей, он испытывает одновременное действие нескольких сил. А если на материальную точку действует несколько сил, то результатом их действия будет одна равнодействующая сила, которая находится векторным сложением исходных сил:

$$\overrightarrow{F}_{равн} = \overrightarrow{F}_{1}+\overrightarrow{F}_{2}+…$$

Сила, действующая на заряд, равна произведению напряженности поля на величину заряда:

$$\overrightarrow{F}_{n} = { \overrightarrow{E}_{n} q}$$

Поскольку заряд в рассматриваемой ситуации один и тот же, то:

$$\overrightarrow{F}_{равн} = (\overrightarrow{E}_{1}+\overrightarrow{E}_{2}+…)q$$

Принцип суперпозиции

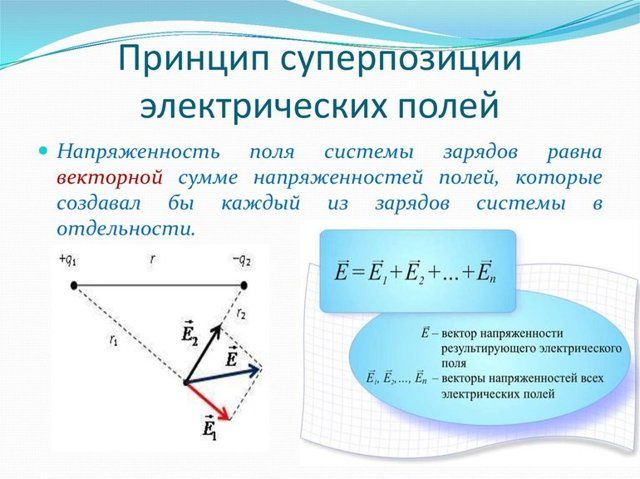
Выражение в скобках представляет собой векторную сумму напряженностей всех полей, действующих на заряд. Получается, что результат действия на заряд нескольких полей эквивалентен действию одного поля, напряженность которого равна векторной сумме напряженностей всех полей, действующих на заряд. Иначе можно сказать, что результирующее поле, существующее в точке, является векторной суммой всех полей, его составляющих. В этом и состоит принцип суперпозиции (наложения) полей.

То есть, формула принципа суперпозиции полей записывается следующим образом:

$$\overrightarrow{E}_{общ}=\overrightarrow{E}_{1}+\overrightarrow{E}_{2}+…$$

Отметим, что потенциал результирующего поля не обязательно равен сумме потенциалов исходных полей. Это происходит потому, что потенциал – скалярная величина, не учитывающая направление.

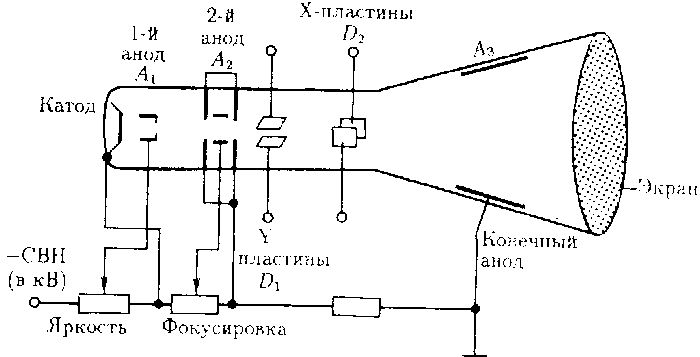
Принцип суперпозиции полей позволяет не только находить напряженность поля, создаваемые несколькими зарядами. Гораздо чаще возникает ситуация, когда заряд распределен по телу неравномерно. В этом случае тело можно разбить на множество элементарных тел, каждое из которых имеет свой заряд, отличный от прочих. А потом поле в любой точке пространства вычисляется, как векторная сумма полей всех элементарных зарядов. При уменьшении размера элементарного тела до нуля сумма заменяется интегралом по объему. Данный способ используется при определении картины картину сложных электрических полей, например, при проектировании электровакуумных приборов.