
Закон Кулона, описывающий взаимодействие зарядов, относится к двум точечным зарядам. Однако в реальности такая ситуация крайне редка: как правило, реальные заряды точечными не являются, и их количество больше двух. Для определения сил взаимодействия в этом случае необходимо использовать принцип суперпозиции. Кратко рассмотрим принцип суперпозиции электрических полей.
Для разных случаев результат совместного действия многих сил должен рассчитываться по-разному. Но наиболее часто употребляемым и наиболее интуитивно понятным является принцип суперпозиции.
Формулировка принципа суперпозиции следующая: результат нескольких величин, действующих одновременно, равен сумме исходных величин.
При этом необходимо помнить два важных момента:
- Сумма должна учитывать характер складываемых величин. Например, для скалярных неотрицательных величин используется обычная арифметическая сумма. Если величины могут быть как положительными, так и отрицательными, сумма должна быть алгебраической. Наконец, для векторных величин необходимо использовать векторные правила сложения.
- Несмотря на свою кажущуюся очевидность, принцип суперпозиции не является универсальным. Он может применяться только в случае линейных и потенциальных взаимодействий. Линейное поле не влияет само на себя, а в потенциальном поле работа силы зависит только от начальной и конечной точки траектории. Например, поле сил трения не является потенциальным, и принцип суперпозиции для сил трения не выполняется.
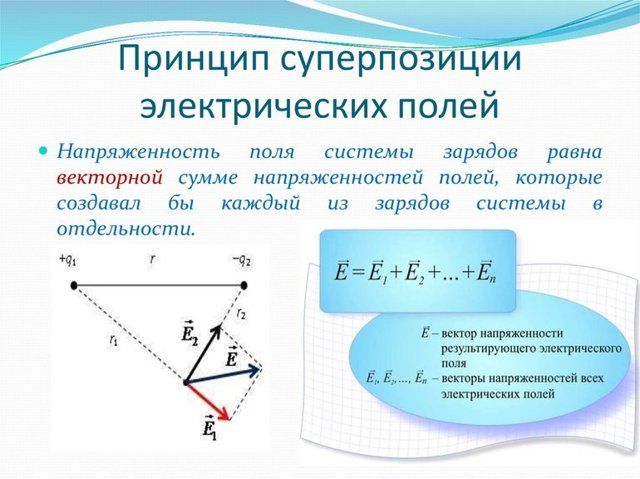
Принцип суперпозиции в электростатике
Проверим, допустимо ли применять принцип суперпозиции для электрических полей.
Электрическое поле характеризуется такими параметрами, как напряженность и потенциал. Первая величина — векторная, вторая —скалярная. Следовательно, при суммировании напряженностей необходимо использовать правила векторной арифметики, а при суммировании потенциалов достаточно алгебраического сложения.
Электрическое поле линейно и потенциально. А значит, к нему можно применять принцип суперпозиции. В виде формулы для напряженности электрического поля он выглядит так:
$$\overrightarrow E_{общ}= \overrightarrow E_1+\overrightarrow E_2+…+\overrightarrow E_n$$

Для потенциала электрического поля принцип суперпозиции может быть выражен формулой:
$$varphi _{общ}= varphi_1+varphi_2+…+varphi_n$$
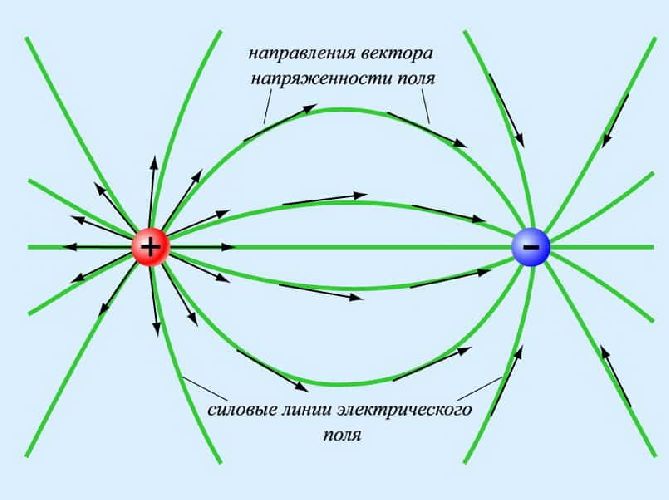
Принцип суперпозиции также позволяет определить напряженность или потенциал поля, источником которого является не точечный заряд, а заряд, распределенный по телу.
В этом случае все тело разбивается на множество мелких областей, в каждой из которых заряд считается одинаковым, вычисляется напряженность и потенциал каждой области в рассматриваемой точке, а потом все потенциалы и напряженности складываются. В результате можно получить полную картину электрического поля такого тела с неравномерно распределенным зарядом, построить эквипотенциальные поверхности и линии напряженности.
Что мы узнали?
Если электрическое поле в точке порождается несколькими зарядами, то для определения его напряженности и потенциала необходимо использовать принцип суперпозиции. Суммарная напряженность равна векторной сумме исходных напряженностей. Суммарный потенциал равен алгебраической сумме потенциалов.








Комментирование закрыто