
Потенциальная энергия наравне с кинетической энергией является одним из ключевых понятий физики. Понимание ее сути существенно облегчает решение ряда прикладных задач и позволяет прийти к важнейшему закону природы – закону сохранения энергии
$A=FS=mgS$.
При достаточно малом S силу тяжести с определенной точностью можно считать постоянной. Если перемещение происходит по вертикали, то $S=h_2 – h_1$. Если тело скатывается по наклонной поверхности, то перемещение равно $lcos varphi$. Но это произведение равно высоте, на которую опустилось тело. То есть работа в поле тяжести определяется только начальным и конечным положением тела. Поэтому:
$A = mgh_2 – mgh_1$.
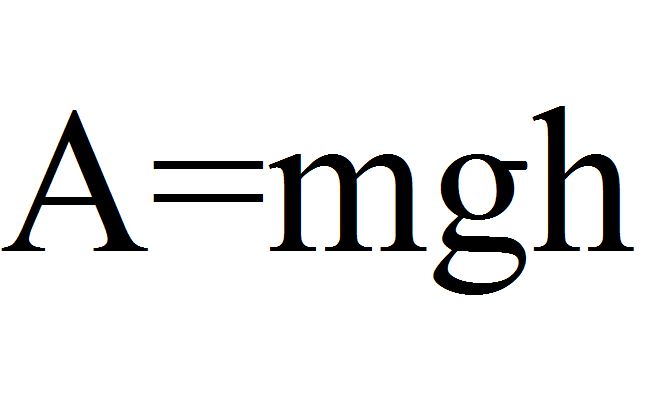
Произведение силы тяжести на высоту называют потенциальной энергией тела в поле тяжести. В данном случае $mgh_1$ принято за потенциальную энергию нулевой точки.
Так как нулевая точка выбирается произвольно, значение потенциальной энергии в любой точке определяется с точностью до константы. В строгом виде формула потенциальной энергии будет такой: $V = mgh + C$.
В физическом смысле С – часть потенциальной энергии, которая запасена телом в нулевой точке. Если рассматривать разность потенциальных энергий относительного одного и того же нулевого уровня, то константы сокращаются. Поэтому определение абсолютного значения потенциальной энергии чаще всего не нужно.
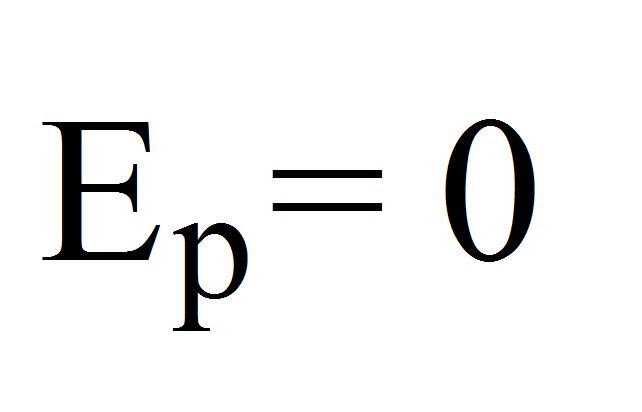
Потенциальная энергия упругой деформации
Рассмотрим пружинный маятник, а точку х=0 будем считать нулем. Работа по перемещению груза, прикрепленного к пружине, определяется формулой: $A= int_0^x kxdx = {1 \over 2}kx^2$, где kx – сила упругости. В общем случае работа – всегда интеграл. Выражение ${1 \over 2}kx^2$ называют потенциальной энергией упругой деформации, и зависит оно только от положения груза относительно нулевой точки и не зависит от периода изменения.
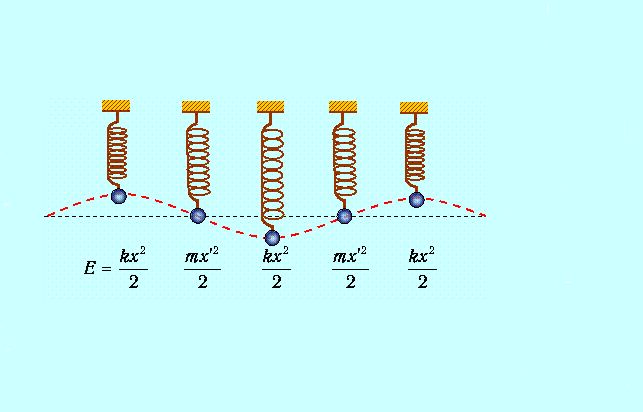
Для обоих рассмотренных случаев (работа в поле силы тяжести и работа упругой деформации) общим является одно: если тело, начав движение в начальной точке, в конце концов вернулось в нее же, то общая работа равна нулю.
По этому правилу легко проверить, консервативная сила или нет. К консервативным, помимо упомянутых, относится также сила кулоновского взаимодействия.
Задачи
- Альпинист массой 70 кг находится в штурмовом лагере, на высоте 5200 метров. Высота вершины – 6100. Найти его потенциальную энергию в каждой точке, приняв за нулевую точку уровень моря. Найти работу против силы тяжести, которую совершит альпинист, совершив переход от штурмового лагеря до вершины.
Решение первой задачи
В нулевой точке потенциальная энергия принимается равной нулю. Тогда в штурмовом лагере потенциальная энергия альпиниста относительного нулевого уровня равна:
$V_1 = mgh_1 = 70g5200 = 3640 кДж$
А на вершине:
$V_2 = mgh_2 = 70g6100 = 4270 кДж$
Работа же равна разности минимальной потенциальной энергии и максимальной:
$A = mgh_2 – mgh_1 = 4270 – 3640 = 630 кДж$
- Деформация пружины маятника равна 5 см, жесткость пружины равна 100 Н/м. Найти потенциальную энергию груза в момент, когда деформация максимальная.
Решение второй задачи
Предполагая, что в х=0 потенциальная энергия равна нулю, запишем:
$V= {1 \over 2}kx^2 = {{100 cdot 0,0025} \over 2} = 0,125 Дж$ – потенциальная энергия в точке максимальной деформации.
Что мы узнали?
В ходе урока было выяснено, что такое потенциальная энергия в общем случае (функция, зависящая от координат), рассмотрены потенциальные энергии в поле тяжести и при упругих деформациях и выведены формулы расчета. В закрепление материала были приведены примеры решения двух простых задач на разные виды потенциальной энергии.








Комментирование закрыто