Первая космическая скорость

Почему брошенный камень всегда падает на Землю, а космические орбитальные станции способны долгое время летать вокруг Земли не падая? Причина кроется в скорости полета орбитальных станций, которая гораздо выше скорости полета брошенного камня. Найдем эту скорость.

Если представить себе Землю в виде шара, на вершине которого находится гора с пушкой, то при достаточно высокой скорости он упадет Землю «сбоку». А при еще большей скорости – «снизу». Наконец, при еще более высокой скорости он совершит полный круг и попадет в пушку с другой стороны. Если к тому времени убрать пушку – то он продолжит полет вокруг Земли по круговой траектории.

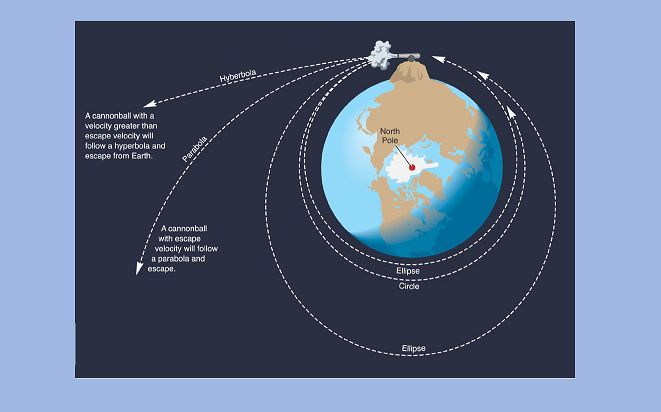
Заметим, что импульс скорости для снаряда требуется только один раз – при запуске. В дальнейшем снаряд будет постоянно двигаться по круговой траектории вокруг Земли. Земля постоянно будет притягивать снаряд, сообщая ему центростремительное ускорение, и снаряд постоянно будет падать на Землю, но за счет кривизны Земли – никогда не упадет.

Такой мысленный эксперимент впервые был проделан И. Ньютоном, поэтому он называется «Гора Ньютона».

Первая космическая скорость

Таким образом, космическая станция, также, как и брошенный камень, постоянно падает на Землю, но за счет большой орбитальной скорости это падение никогда не кончается.

Для нахождения Первой Космической скорости необходимо учесть, что она должна быть такой, чтобы создаваемое при этом центростремительное ускорение было бы равно ускорению свободного падения ($a_ц = mathrm{g}$). Под действием такого центростремительного ускорения траектория полета будет окружностью.

Центростремительное ускорение, действующее на тело, равно:

$$a_ц={v^2\over R},$$

где:

• $v$ – величина мгновенной скорости тела;
• $R$ – радиус вращения (он равен сумме радиуса Земли и высоты орбиты ($R = R_З+h$).

Пусть тело имеет массу $m$, тогда согласно Закону Всемирного Тяготения, сила притяжения равна:

$$F=G{M_З m\over R^2},$$

где:

• $G$ – гравитационная постоянная;
• $M_З$ – масса Земли.

По Второму Закону Ньютона эта сила создает ускорение свободного падения:

$$mathrm{g}={F\over m}=G{M_З\over R^2}$$

Именно оно и является центростремительным. Таким образом:

$${v^2\over R}=G{M_З \over R^2}$$

Или:

$$v=sqrt{G{ M_З \over R}}$$

Поскольку более известным параметром земного тяготения является ускорение свободного падения, то массу Земли можно выразить через него:

$$M_З = {mathrm{g} R^2\over G}$$

И, таким образом:

$$v=sqrt{mathrm{g}R}$$

Для Земли Первая Космическая скорость равна $v ≈ 8 км/с$.

Если скорость тела увеличивать выше этого значения, то траектория превратится во все более вытянутый эллипс. Скорость в $sqrt 2$ раз больше Первой Космической называется Второй Космической. При такой скорости траектория превратится в параболу, и тело навсегда сможет покинуть планету. Для Земли Вторая Космическая скорость равна 11.2 км/с.