Период свободных колебаний

Свободные колебания – это колебания системы под действием только внутренних сил. Одним из важнейших параметров колебаний является период колебаний. Рассмотрим это понятие более подробно, его формулу и возможность измерения.

Флаг на ветру – это пример вынужденных колебаний. Он колеблется исключительно под воздействием ветра. Маятник – пример свободных колебаний. Нитяной маятник колеблется под действием силы тяжести, причина которой – масса самого маятника. Пружинный маятник колеблется под воздействием силы упругости, причина которой – внутренние напряжения деформации пружины.

Условия возникновения свободных колебаний

Для того, чтобы в системе могли возникать свободные колебания, необходимо выполнение следующих условий:

• в системе должно быть одно положение равновесия;
• система должна быть выведена из положения равновесия;
• в системе должна возникать сила, возвращающая систему в положение равновесия;
• потери энергии в системе должны быть малы.

Для примера можно рассмотреть пружинный маятник. В нем выполняются все эти условия.

Заметим, что сила, которая стремится возвратить маятник в положение равновесия, зависит от отклонения маятника, и тем больше, чем больше это отклонение. А значит, и ускорение, которое получает масса пружинного маятника, будет направлено к положению равновесия, и зависеть от отклонения. Ускорение – это вторая производная перемещения. Единственная функция, вторая производная которой пропорциональна самой функции – это круговая функция (синус или косинус). Колебания, происходящие по закону круговой функции, называются гармоническими. Такими колебаниями являются колебания пружинного маятника. Их формула:

$$x(t)=A cos sqrt{k\over m}t$$

где:

• $x$ – перемещение маятника в момент $t$;
• $A$ – амплитуда колебаний маятника;
• $k$ – жесткость пружины маятника;
• $m$ – масса маятника;

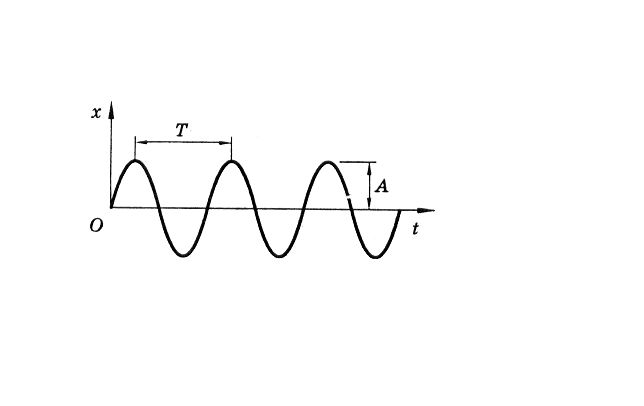
График колебаний:

Период свободных колебаний

Период колебаний – это время, за которое совершается одно колебание. Поскольку колебания маятника описываются круговой функцией, то ее период равен периоду этой функции.

$$T=2pisqrt {m\over k}$$

То есть, зная жесткость пружины и массу маятника, можно получить период.

Период колебаний можно измерить и непосредственно. Если посчитать количество колебаний $N$ за время $t$, отношение этих величин также даст период свободных колебаний маятника:

$$T={t\over N}$$

Зная период колебаний маятника и его массу, можно определить жесткость пружины.

Период колебаний обычного нитяного маятника можно использовать для нахождения ускорения свободного падения $mathrm{g}$, поскольку формула периода свободных колебаний нитяного маятника аналогична формуле периода колебаний пружинного маятника:

$$T=2pisqrt {l\over mathrm{g}}$$

При этом необходимо учесть ограничения формулы – максимальное отклонение нитяного маятника должно быть намного меньше его длины.