
Движение, при котором траектория представляет собой прямую линию, называется прямолинейным. Если при таком движении скорость равномерно изменяется, то изменение скорости за единицу времени называется ускорением, а такое движение называется равноускоренным. Рассмотрим перемещение при прямолинейном равноускоренном движении.
Если бы движение было равномерным, то материальная точка каждую секунду проходила бы одно и то же расстояние. Однако для равноускоренного движения это не так.
Найдем формулу перемещения тела при прямолинейном равноускоренном движении.
Вывод формулы перемещения
Наиболее просто найти формулу перемещения из графика скорости. Перемещение материальной точки равно площади фигуры, лежащей под графиком скорости.
Например, для равномерного движения график скорости представляет горизонтальную прямую, а значит, площадь под этим графиком является прямоугольником, высота которого равна скорости, а ширина – времени. Для нахождения его площади необходимо перемножить эти величины, получив известную формулу «расстояние равно произведению скорости на время пути».
При равноускоренном движении скорость равномерно меняется, а значит, ее график представляет собой наклонную прямую:
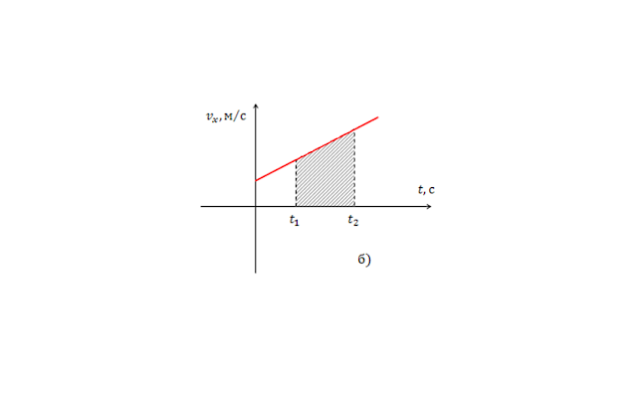
Найдем площадь фигуры под этой прямой.
Фигура является четырехугольником, одна сторона является отрезком оси абсцисс длинной $Δt=t_2-t_1$, две соседние стороны – вертикальные отрезки, длина каждого равна значению скорости в соответствующий момент времени: $v_1$ и $v_2$. То есть, фигура является трапецией, площадь которой, как известно из геометрии, равна произведению полусуммы оснований на высоту. Высота равна промежутку времени, основания – скоростям вначале и в конце пути. То есть, если начальный момент времени нулевой ($t_1=0$), а скорость в начальный момент обозначить $v_0$ то рассматриваемое перемещение равно:
$$x(t)={v+ v_0\over 2}t$$
Поскольку при равноускоренном движении скорость за единицу времени увеличивается на величину ускорения, то скорость в момент $t$ будет равна сумме начальной скорости и произведению ускорения на время пути:
$$v(t)= v_0 + at$$
Подставив значение скорости в предыдущую формулу, и приняв, что перемещение в начальный момент времени было равно $x_0$, получим окончательную формулу перемещения тела при прямолинейном равноускоренном движении:
$$x(t)=x_0+v_0t+{at^2\over 2}$$
Из вида формулы можно заключить, что график перемещения при равноускоренном движении является параболой.
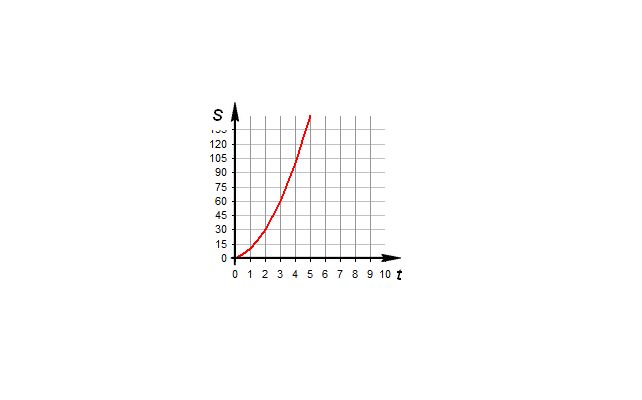
При решении задач время движения зачастую неизвестно, в этом случае удобно выразить его из предыдущей формулы, получив соотношение:
$$x(t)=x_0+{v^2-v_0^2\over 2a}$$
Парабола имеет, как правило, два корня. А значит, задачи о перемещении тела при равноускоренном движении могут иметь не одно, а два правильных решения. Например, если найти время, когда предмет, брошенный вверх со скоростью 20м/с достигнет высоты 9 м, мы получим два ответа: через 0.52 с и 3.56 с. Оба эти ответы правильны. Предмет будет на высоте 9 м дважды – первый раз при полете вверх, второй раз в момент падения.
Что мы узнали?
Наиболее частый пример прямолинейного равноускоренного движения – это свободное падение тел, пока сопротивление воздуха пренебрежительно мало. Перемещение при равноускоренном прямолинейном движении является квадратичной функцией, ее график является параболой.








Комментирование закрыто