
Наряду с законами Ньютона тема относительности движения является одной из важнейших в курсе классической физики. Инвариантность законов механики позволяет произвольно выбирать инерциальную систему отсчета, что упрощает решение многих задач, особенно задач на вращение тел.
Принцип относительности
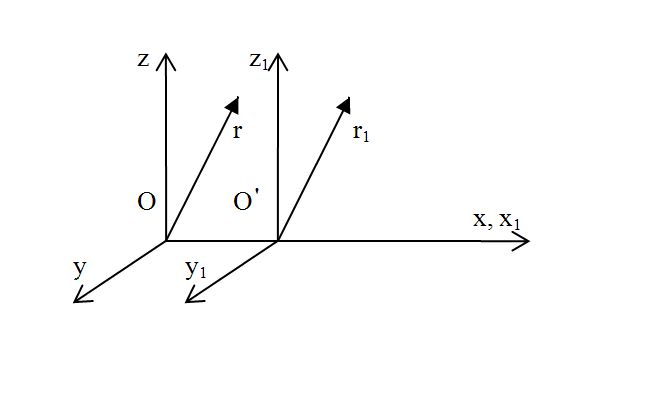
Галилей задал следующий вопрос: буду ли разными законы механики при переходе между инерциальными системами координат? Ответим на него. Для этого введем две системы отсчета: неподвижную О(x, y, z) и О’(x’, y’, z’), которая движется вдоль оси Ох равномерно и прямолинейно со скоростью υ.

Вектор ОО’ соединяет начало обеих систем координат. В О (x, y, z) положение точки определяется r, в О’ (x’, y’, z’) – радиус-вектором r’.
$vec{r}={vec{OO’} + vec{r’}}$ – связь координат точки в разных система отсчета.
Но поскольку $vec{OO’}={vec{v}t }$, то:
$$vec{r}={vec{r’} + vec{v}t}$$ (1)
Производная функции по переменной – это скорость изменения функции. Операция взятия производной называется дифференцированием.
Таким образом, производная функции r по переменной t есть скорость движения материальной точки, то есть быстрота изменения координаты точки. Продифференцировав (1), получаем:
$vec{V}={vec{v’} + vec{v}}$ (2) – закон, по которому производится сложение скоростей.
Суммирование векторных величин выполняется по правилу треугольника или параллелограмма.
Производная скорости по времени – это ускорение. В случае, если движение не равноускоренное, производная скорость равна нуля, что ясно из определения – изменения функции нет, он постоянна. Тогда из (2) получаем:
$vec{а}=vec{а’}$, а значит и $vec{F}=vec{F’}$. Независимо от выбора между инерциальными системами отсчета законы механики будут одинаковым. В этом заключается принцип относительности Галилея. Он является частным случаем принципа относительности Эйнштейна, который говорит, что все законы, а не только законы механики, одинаковы в инерциальных системах отсчета.
Уравнение (1) можно расписать в проекциях:
$$vec{x}={vec{x’} + vec{v}t}$$
$$vec{y}=vec{y’}$$
$$vec{z}=vec{z’}$$
К этим уравнениям обычно дописывают $vec{t}=vec{t’}$
Вместе эти четыре уравнения дают классическое преобразование координат Галилея для прямолинейного движения с постоянной скоростью одной системы отсчета относительно другой.
Задачи
- Велосипедист движется вдоль трамвайных путей со скоростью υ1. На встречу ему проезжает товарный поезд. Время, в течение которого велосипедист наблюдал поезд, равно t. Длина поезда – L. С какой скоростью двигался поезд?
Решение первой задачи
Согласно закону сложения скоростей получаем:
$vec{V}={vec{v_1} + vec{v}}$ – скорость сближения велосипедиста и поезда.
$vec{r}={(vec{v_1} + vec{v})t}$ – расстояние, которое будет пройдено за t при скорости V. Приравняв к длине поезда, выразим скорость поезда:
$v=frac{L}{t} – {v_1}$ – окончательный ответ.
- Человеку необходимо переплыть на другую сторону реки по линии, строго перпендикулярной к берегу. Скорость течение – υ1, скорость движения человека – υ2. Под каким углом к перпендикуляру необходимо плыть?
Решение второй задачи
Составим прямоугольный треугольник на векторах υ1 и υ2, которые будут его катетами.

Из него найдем:
$sin alpha=frac{v_2}{v_1}$, тогда $alpha=arcsin frac{v_2}{v_1}$
Что мы узнали?
В ходе урока было выяснено, что всякое движение относительно, а законы механики инварианты, были выведены уравнение, связывающее координаты точки в разных системах координат, закон сложения скоростей и преобразования Галилея.








Комментирование закрыто