
В реальной жизни приходится иметь дело с телами, скорость движения которых может меняться на разных участках пути. Описание такого движения несколько сложнее и требует введения новых понятий.
и это средняя скорость на всем пути.
Иногда пользуются средней путевой скоростью, которую можно найти так:
Индексами здесь обозначены участки пути.

С изобретением дифференциального исчислением сэром Исааком Ньютоном в физике получили распространение другие величины, которыми стали описывать неравномерное движение. Это:
- Радиус-вектор перемещения;
- Мгновенная скорость;
- Мгновенное ускорение.
Каждое следующее понятие вводится через предыдущее. Поэтому сначала разберемся с радиус-вектором. Под ним понимают направленный отрезок, соединяющий начало координат с точкой, в которой находится тело в данный момент времени.
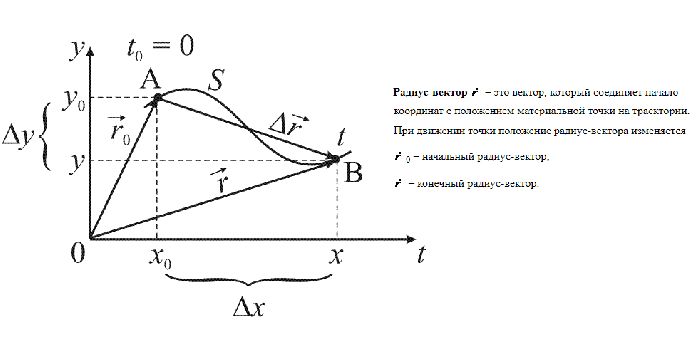
Первую производную радиус-вектора называют мгновенной скоростью. В общем случае она находится по формуле:
Вторую производную радиус-вектора перемещения называют мгновенным ускорением. Формула, по которой его можно найти, в общем виде записывается так:
Посредством двойного интегрирования ускорения можно найти общее уравнение движения.
Виды неравномерного движения
Поскольку скорость – это векторная величина, у нее есть компоненты. В трехмерном пространстве – это x, y, z. В зависимости от характера изменения скорости различают следующие виды:
- Равноускоренное движение;
- Движение с переменным ускорением;
- Движение по окружности с ускорением;
- Движение по окружности с переменным ускорением;
- Движение тела, брошенного под углом.
В первом случае уравнение движения выглядит так:
В случае, если ускорение изменяется, вместо $vec a$ подставляют закон, по которому происходит изменение.
Для движения по окружности вводят три новых понятия: угол поворота ($phi$, радиан), угловая скорость ($omega$, радиан/с) и угловое ускорение ($omega, радиан/с^2$). Уравнение движения по окружности с постоянной угловой скоростью:
Несмотря на то, что линейная скорость ($vec v = [vec omega, vec R]$, где квадратными скобками обозначено векторное умножение) изменяется по направлению, движение по окружности с постоянной угловой скоростью считается равномерным, поскольку за равные промежутки времени точка проходит равные участки пути. Другие случаи движения по окружности отличаются введением углового ускорения по аналогии с равноускоренным движением по прямой.
Когда же тело бросают под углом к горизонту, его движение происходит в поле силы тяжести. Рассмотрим простейший случай, когда иксовая компонента скорости остается постоянной, а меняется только игриковая. Тогда движение описывают системой уравнений:
begin{equation*}
r(t) = begin{cases}
x = v_0 cdot cosphi cdot t\
y = v_0 cdot sinphi cdot t – frac {g cdot t^2}{2}
end{cases}
end{equation*}
$$

Приняв угол равным 90˚, получим случай движения тела, брошенного вертикально вверх.
Задачи
- Две пятых пути автомобиль проехал со скоростью 120 км/ч, одну пятую – со скоростью 60 км/ч, и последнюю часть пути – со скоростью 80 км/ч. Найти среднюю путевую скорость.
Решение:
Запишем общую формулу для нахождения средней путевой скорости:
$v = frac {S_1 + S_2 + S_3}{t_1 + t_2 + t_3}$t
Приняв весь путь за x, напишем:
$S_1 = 2x/5$, $t_1 = 2x/5v_1$
$S_2 = x/5$, $t_2 = x/5v_2$
$S_3 = 2x/5$, $t_3 = 2x/5v_3$
Тогда средняя путевая скорость:
$v = frac {x}{2x/5v_1 + x/5v_2 + 2x/5v_3}$
$v = frac {5}{2/v_1 + 1/v_2 + 2/v_3} = frac {5}{2/120 + 1/120 + 1/40} = frac {5}{1/20} = 100 км/ч$
Что мы узнали?
В ходе урока рассмотрели основные понятия, связанные с неравномерным движением, привели различные примеры неравномерного движение и уравнения, описывающие их. В завершении урока решили задачу на среднюю путевую скорость.








Комментирование закрыто