Механические колебания и волны

Колебательные процессы являются одними из самых распространенных в Природе. Одним из видов этих процессов являются механические колебания и волны. Рассмотрим эту тему подробнее.

Необходимо отметить также, что в первом случае колебания являются периодическими – каждое из них очень напоминает любое другое. А в случае флага на ветру – колебания являются непериодическими, движение точек хотя и происходит вокруг среднего положения, отдельные части этого движения, совершенные в различное время, совсем не похожи друг на друга.

Механические колебания, как и любые другие могут быть свободными, а могут быть вынужденными. Свободные колебания – это колебания, совершаемые под действием внутренних сил системы (пружинный маятник), вынужденные колебания совершаются под воздействием внешней силы (поршень в двигателе).

Если к системе не подводится внешней энергии, а в системе имеются потери (например, на трение), то колебания в такой системе будут затухающими.

Механические волны

Во многих случаях отдельные точки системы, хотя и совершают периодические колебания одинаковой амплитуды и частоты, делают это несинхронно. В первый момент воздействия на систему, из положения равновесия выходят только некоторые точки. Эти точки влияют на соседние, соседние точки тоже начинают выходить из положения равновесия, но делают это с некоторой временной задержкой. В свою очередь эти точки выводят из положения равновесия более далекие точки. В результате к тому времени, как первая точка начнет возвращаться к положению равновесия, другие точки системы будут все еще увеличивать отклонение. Причем, чем дальше точка будет находиться от первоначальной, тем больше будет ее запаздывание.

Гармонические колебания и волны

При изучении колебаний можно убедиться, что большинство из них совершаются по простому закону круговых математических функций – синуса или косинуса. Такие колебания называются гармоническими. В математике доказывается, что любые колебания можно представить бесконечной суммой гармонических составляющих. Поэтому в первую очередь изучаются именно они.

Формула механических колебаний и волн представляет собой следующее соотношение:

$$X=Asin(omega t+phi)$$

где:

• $X$ – координата колеблющейся точки в момент времени $t$.
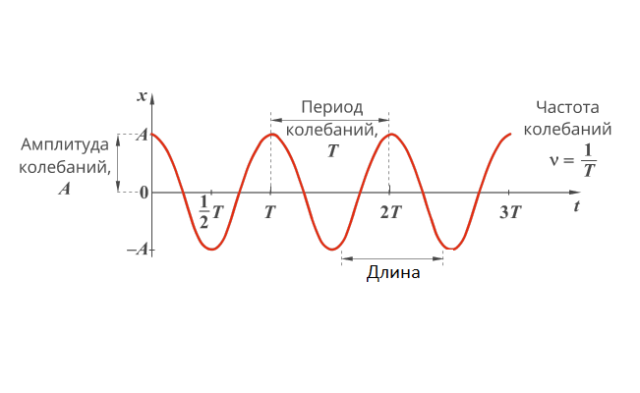
• $А$ – амплитуда колебаний, максимальное отклонение точки в процессе колебания.
• $omega$ – частота колебаний, «скорость», с которой они совершаются.
• $phi$ – начальная фаза колебаний, начальное положение точки в момент времени $t=0$

Время, за которое совершается одно полное колебание, называется периодом колебаний $T$:

$$T={2pi\overomega}$$

Распространение колебаний в виде волн происходит с конечной скоростью $v$. А значит, точки с одинаковой фазой (с одинаковым отклонением от равновесия), будут находиться на некотором расстоянии друг от друга, называемым длиной волны $lambda$:

$$lambda = vT$$