
Любое физическое тело представляет собой набор веществ (одного или нескольких), которые состоят из молекул и атомов. Если тело как целое находится в состоянии покоя, то это не значит, что молекулы вещества “замерли” и не двигаются. Такая ситуация возможна только, если температура тела станет равна абсолютному нулю, то есть Tтела = 00К, а при любой температуре, больше нуля, частицы вещества непрерывно, хаотически двигаются с различными скоростями, поэтому полная кинетическая энергия вещества равна сумме кинетических энергий всех частиц.
$ Е^п_к = Е_1+ Е_2 + Е_3 +…. Е_N $ (2),
где N — полное число частиц в веществе.
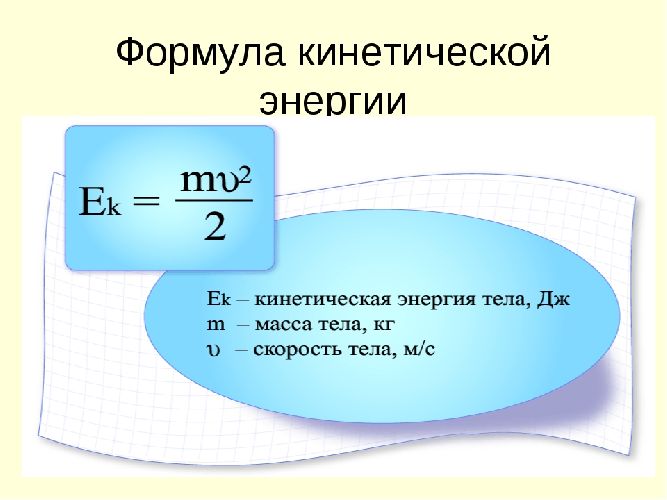
Понятно, что для вычисления кинетической энергии всего вещества по формуле (2) необходимо знать скорости всех частиц, их массы и общее количество. Но это в принципе нереально хотя бы потому, что в одном моле вещества находится гигантское количество молекул — 6,023*1023 !
Эксперименты показывали, что чем сильнее нагрето вещество, тем быстрее (“энергичнее”) двигаются частицы. Например, исследователи могли это видеть, наблюдая броуновское движение в микроскоп. После изобретения итальянским ученым Галилео Галилеем (1564-1642 г.г.) термометра у физиков появилась возможность проводить измерения величины, названной температурой, которая показывала степень теплового состояния вещества.
Общая кинетическая энергия непрерывного хаотического движения всех частиц входит в состав внутренней энергии вещества, которая кроме кинетической включает в себя:
- Потенциальную энергию частиц, вызванную силами межмолекулярного взаимодействия;
- Энергию электронов в атомах;
- Ядерную энергию.
Что же такое температура?
В молекулярно-кинетической теории теплота рассматривается как одна из форм энергии, а именно — кинетическая энергия атомов и молекул. Чем “горячее” тело, тем с большей скоростью двигаются молекулы вещества и, значит, больше становится их кинетическая энергия. Эта величина, будучи усредненной по всему числу беспорядочно движущихся частиц, и есть температура тела (вещества).
Вместо того, чтобы пытаться вычислить энергию по формуле (2), физиками были получены математические формулы, связавшие кинетическую энергию Епк вещества и температуру T. Использование понятия температуры, которое распространяется на все вещества — газообразные, жидкие и твердые, позволило решить задачу по определению энергии Епк.
Как перейти от температуры к энергии
Для измерения энергии в Международной системе СИ используется единица измерения джоуль (Дж), а температура, как известно, измеряется в градусах. Как количественно связаны эти величины? На примере одноатомного идеального газа попробуем получить формулу, связывающую эти величины.
Напомним, что температура в системе СИ измеряется в градусах Кельвина. Связь температуры в градусах Кельвина и температуры в единицах энергии (Дж) выражается формулой:
$ θ = k * T $ (3),
где: k =1,38*10-23 Дж/К — постоянная Больцмана.
Для идеального газа справедлив закон Клапейрона-Менделеева, выражаемый в виде уравнения состояния:
$ p * V = {m\over μ} * R * T $ (4),
где:
p, m и V — давление, масса и объем газа, μ — молярная масса газа,T — температура в градусах по шкале Кельвина, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
В то же время газовая постоянная R равна:
$ R = k * N_a $ (5),
где: k — постоянная Больцмана, Na = 6,023*1023 — число Авогадро, количество молекул в одном моле вещества. Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
$ {m\over μ} * {Na\over V } = n $ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$ p = n * k * T $ (6).
Для давления одноатомного идеального газа воспользуемся выражением:
$ p = {1\over 3} * n * m * v^2_c $ (7),
где: v2c — средний квадрат скорости по всем группам молекул. Напомним, что молекулы в газе двигаются с разными скорости. Распределение по скоростям, то есть количество молекул с определенной скоростью, имеет колоколообразный вид, и впервые было получено английским физиком Максвеллом.
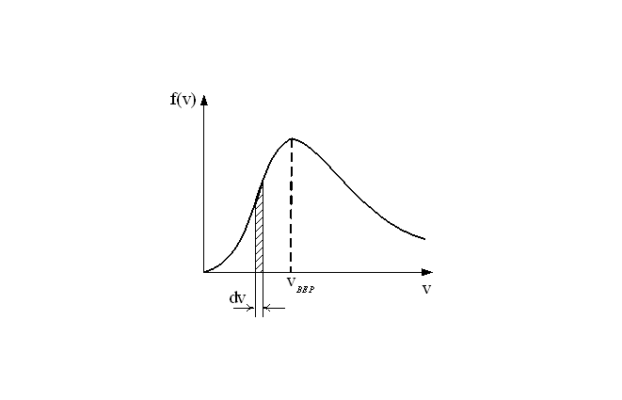
Из формул (6), (7) и выражения (1) для кинетической энергии Ек, получим:
$ Ек = { 3 \over 2} * k * T $ (8).
Уравнение (8) устанавливает однозначную связь между средней кинетической энергией вещества и его абсолютной температурой.
Если газ будет не одноатомный, то часть энергии уйдет на колебания атомов внутри молекул и на вращение самих молекул. Колебания и вращения тоже обусловлены движением частицы, но выражения для этих составляющих энергии будут несколько иные. Формулы (1) и (7) получены в предположении, что одноатомные частицы двигаются только поступательно.
Что мы узнали?
Итак, мы узнали что кинетическая энергия веществ, представляет собой сумму кинетических энергий всех частиц вещества. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. Приведена формула, связывающая среднюю кинетическую энергию вещества с температурой.








Комментирование закрыто