Кинематика вращательного движения

Кинематика – это раздел механики, науки о механических движениях тел. Кинематика изучает движение тел, не рассматривая причины этих движений. Познакомимся с кинематикой вращательного движения.

Поэтому кинематические характеристики вращательного движения, хотя и аналогичны кинематическим характеристикам поступательного движения, тем не менее, имеют заметные отличия.

Поскольку при поступательном движении все точки тела движутся одинаково – движение описывается только для одной точки, остальные движутся точно так же. Но что делать, если все точки движутся по-разному ?

Выход из ситуации лежит в нахождении общих параметров движения различных точек, и описание движения с помощью этих параметров. Несмотря на то, что при вращении точки твердого тела движутся по различным траекториям, эти траектории не только являются окружностями с центрами, лежащими на одной прямой, но и при движении по ним точки за равные промежутки времени описывают дуги одинакового угла. Таким образом, если связать движение с углом поворота, можно будет описывать вращения всех точек тела сразу.

То есть, для перехода от описания поступательного движения к вращательному, можно сделать замену характеристик:

• перемещение $x(м)$ заменить на угол $alpha (рад)$;
• скорость $v(м/с)$ заменить на угловую скорость $omega (рад/с)$;
• ускорение $a(м/с^2)$ заменить на угловое ускорение $varepsilon (рад/с^2)$.

Все расчеты вращательного движения производятся для угловых величин, и уже потом, зная угловые характеристики, при необходимости можно найти мгновенные линейные параметры.

Формулы кинематики для вращения

Получим кинематические формулы вращательного движения, произведя описанную замену. Формулы для поступательного движения:

$$x=x_0+v_0t+{at^2\over2}$$

$$v=v_0+at$$

Формулы после замены:

$$alpha=alpha_0+omega_0t+{varepsilon t^2\over2}$$

$$omega=omega_0+varepsilon t$$

Кроме того, при решении задач полезно выразить время из одной формулы, и подставить его в другую, получив соотношение, нередко сильно упрощающее расчеты:

$$alpha ={omega^2-omega_0^2 \over 2 varepsilon}$$

Следует отметить, что формулы для поступательного движения могут иметь векторную форму, все параметры могут быть направлены по-разному. При вращении движение совершается по фиксированной траектории. Поэтому значения в формулах для вращательного движения скалярны. В остальном – аналогия полная.

Связь угловых и линейных значений

При вращательном движении угол и пройденное расстояние прямо пропорциональны, коэффициент пропорциональности равен радиусу $R$. Поэтому для нахождения линейных значений достаточно умножить соответствующие угловые значения на радиус:

• $S = alpha R$
• $v = omega R$
• $a = varepsilon R$

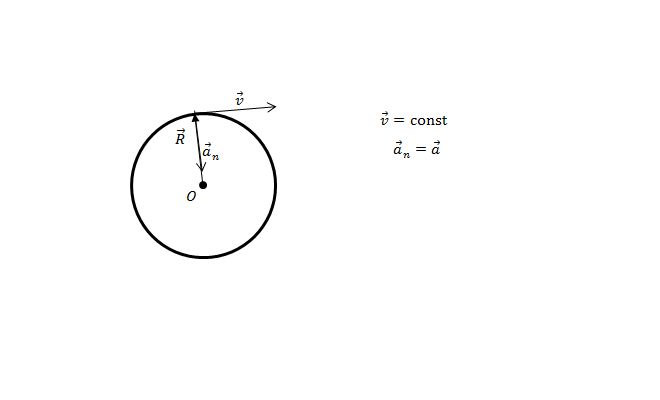
Кроме линейного ускорения, меняющего модуль скорости, на любое вращательное тело также действует центростремительное ускорение, меняющее направление скорости. Оно равно:

$$a_ц = omega_2 R = {v^2\over R}$$