
В цепи постоянного тока катушка индуктивности ведет себя так же, как обычный длинный провод. Однако для переменного тока ситуация существенно иная. Поговорим кратко о катушке индуктивности в цепи переменного тока.
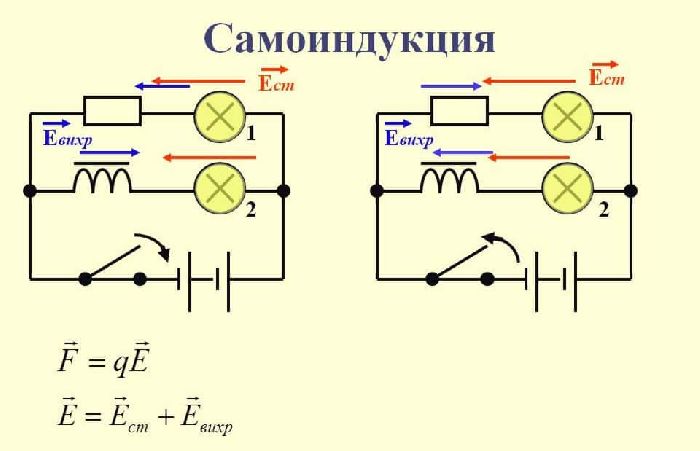
Получается, что катушка «сопротивляется» любым изменениям тока в ней. Если ток возрастает, она не дает ему возрастать. Если ток убывает, она не дает ему убывать. Для переменного тока, который постоянно изменяет свое значение по гармоническому закону, катушка постоянно «сопротивляется». Таким образом, для переменного тока можно говорить об особом, индуктивном, сопротивлении катушки (на постоянном токе это сопротивление равно нулю).
Это сопротивление существенно отличается от сопротивления активного. Если на активном сопротивлении работа тока преобразуется в тепло, то на сопротивлении катушки во время возрастания тока его работа преобразуется в энергию магнитного поля в катушке, а во время убывания она возвращается из магнитного поля в энергию тока. Катушка как бы «имеет реакцию» на изменение тока через нее за счет индуктивности. Поэтому такое сопротивление называется реактивным.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin omega t$$
Мгновенное значение напряжения:
$$u =Lomega I_m cos omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ Lomega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(omega t+{pi \over 2})$$
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода. В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет.
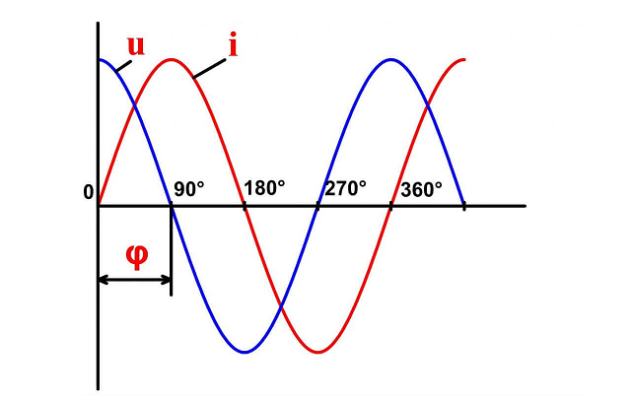
Амплитуда силы тока в катушке равна:
$$I_m={U_m\over omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:

Что мы узнали?
Катушка индуктивности в цепи переменного тока обладает реактивным сопротивлением, пропорциональным частоте. Первую половину периода она запасает энергию электрического тока в виде магнитного поля, а вторую половину периода возвращает эту энергию электрическому току. При этом колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода.








Комментирование закрыто