Фаза колебаний

Любой колебательный процесс, который изучается физикой, имеет ряд параметров, одним из которых является фаза. Кратко рассмотрим, что это такое, каков физический смысл фазы, в чем измеряется фаза, приведем формулу фазы колебаний.

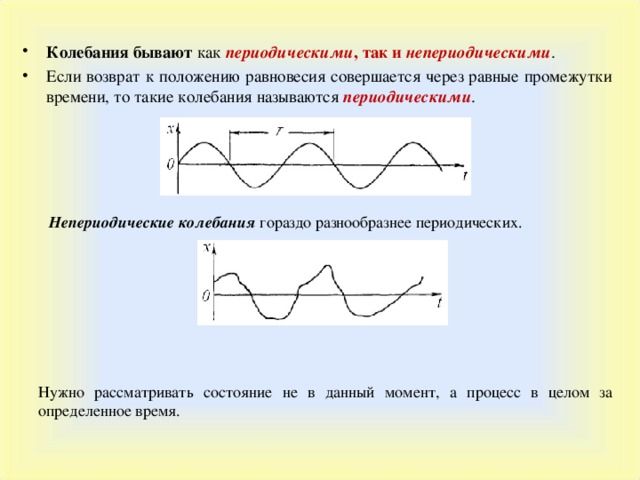
Фаза колебаний

Рис. 1. Периодические и непериодические колебания.

Простейшим периодическим колебанием является колебание, которое совершается по закону круговых функций (синуса или косинуса). Оно называется гармоническим. Поскольку в высшей математике доказывается, что любое колебание (в том числе непериодическое) можно представить в виду бесконечной суммы гармонических колебаний, то в первую очередь изучаются именно они. А по определению любое гармоническое колебание можно представить в виде функции:

$$A=A_0sin Bigg ( {2pi\over T} t +varphi_0 Bigg ),$$

где:

  • $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
  • $T$ — период колебаний;
  • $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
  • $varphi_0$ — начальная фаза колебаний.

Коэффициент ${2pi\over T}=omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2pi\over T} t +varphi_0=varphi$, которое является аргументом функции синуса, называется полной фазой колебания.

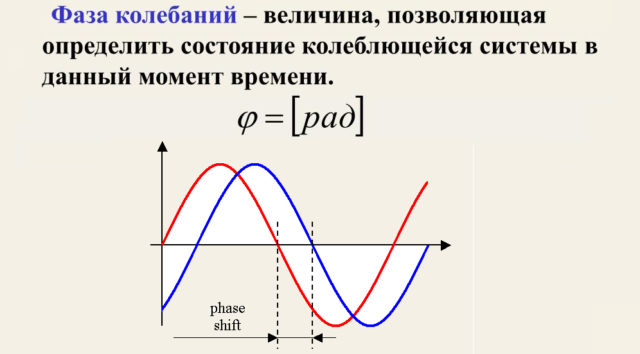
Фаза колебаний

Рис. 2. Фаза колебания.

Фаза гармонического колебания

Из формулы гармонического колебания можно понять физический смысл фазы. Поскольку аргументом функции $sin(x)$ является угол поворота единичного вектора на координатной плоскости, выраженный в радианах, и его период равен $2pi$, то фаза — это часть периода колебания, соответствующая моменту $t$. Она еще выражается в радианах и тоже имеет период $2pi$.

Из формулы также можно видеть, что если $t=0$, то $varphi=varphi_0$ (полная фаза в начальный момент равна начальной фазе).

Разность фаз

Для одного колебательного процесса фаза не играет большой роли. В самом деле, если брать разные моменты времени за начальные, мы можем получать любое значение фазы, колебательный процесс при этом никак не изменится. Однако, когда речь идет о нескольких колебательных процессах, то значение фазы существенно возрастает. Именно фазой определяется разница мгновенных значений двух колебаний.

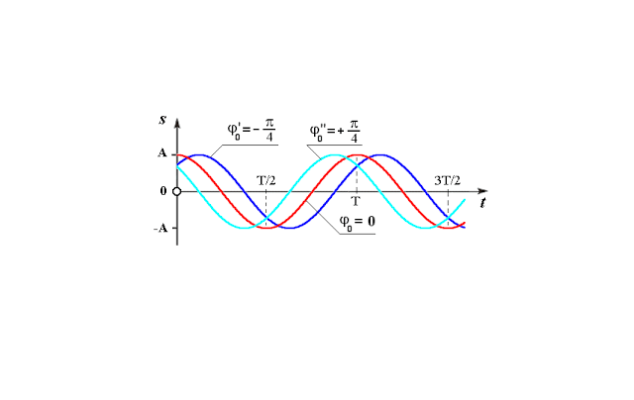
Фаза колебаний

Рис. 3. Графики колебаний с различными фазами.

Если частоты колебаний неодинаковы, то каждый момент времени фазы будут различны, их разность также будет изменяться. Если же частоты колебаний одинаковы, то несмотря на изменение со временем фазы каждого колебания, разность фаз этих двух колебаний будет постоянной. Это может приводить к интересным ситуациям.

Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза будет равна нулю, а у второго — $pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Более того, если эти колебания сложить, то их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противофазе.

Что мы узнали?

Фаза колебания — это часть периода колебания, соответствующая текущему моменту времени. Единица измерения фазы — радиана, она имеет период $2pi$. Особо важное значение имеет разность фаз двух и более колебаний. Если частота этих колебаний одинакова, то и разность фаз будет всегда постоянной.